В конечном счете нам нужен метод типа makeSurfaceMeshO, который генерирует такие сетки для заданной поверхности Р(и, v). Реализация функции, выполняющей такую работу, будет рассматриваться в тематическом задании 6.13.
Отметим, что некоторые графические пакеты содержат подпрограммы, которые в высшей степени оптимизированы, если они работают с треугольниками. Для того чтобы использовать такие подпрограммы, можно «полигонизировать» сферу в совокупность треугольников, разбив каждый четырехугольник на два треугольника.
Проще всего было бы использовать те же вершины, что и раньше, но изменить список граней, заменяя каждый четырехугольник двумя треугольниками. Например, грань с вершинами 2, 3, 15,14 можно было бы разбить на два треугольника с вершинами 2, 3, 15 и 2, 15,14.
Сфера является частным случаем поверхности вращения, которые мы рассматриваем в разделе «Поверхности вращения» Конический цилиндр также является поверхностью вращения. Нетрудно разработать каркасную модель для конического цилиндра. На рис. 6.50 показан конический цилиндр, аппроксимированный при nSlices = 10 и nStacks = 1. В качестве крышки и основания использован октагон (восьмиугольник). Если вы предпочитаете использовать в сетке только треугольники, то стенки, крышка и основание должны быть разбиты на треугольники. (Как?).
Моделирование поверхностей полигональными сетками
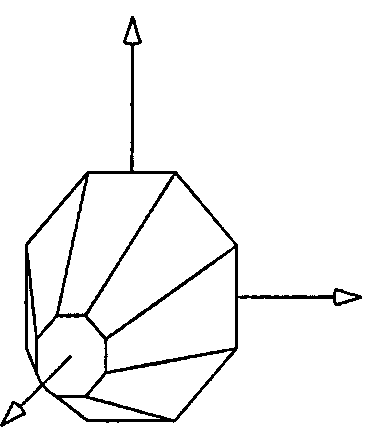
Рис. 6.50. Каркасная аппроксимация конического цилиндра Практические упражнения
6.5.8. Сетка для заданной сферы
Выбрав удобную схему нумерации, составьте списки вершин, нормалей и граней для сферы при nSl ices = 6 и nStacks = 4.
6.5.9. Ограничение сетки треугольными гранями Откорректируйте все списки из предыдущего упражнения для случая, когда все грани являются треугольниками.
6.5.10. Сетка для цилиндра и конуса Напишите списки вершин, нормалей и граней для базового цилиндра при nSlices = 4 и nStacks - 2.
В этом разделе мы продолжаем изучение криволинейных поверхностей и переходим к семейству линейчатых поверхностей (ruled surfaces). Это семейство описывается просто, однако оно содержит большое разнообразие полезных и интересных форм. Мы исследуем, как описывать такие формы, «полиго-низировать» их и вычислять нормальный вектор к ним в любой точке.
