Вообще говоря, частные производные от вектора р(и, V) существуют в* тех случаях, когда поверхность является «достаточно гладкой». Большинство интересующих нас при моделировании сцен поверхностей обладают необходимой гладкостью и описываются достаточно простыми математическими выражениями, поэтому нахождение необходимых частных производных не составляет труда. Поскольку р(м, ь) = Х(и, ь)\ + У(и, V)} + 2{и, v)k, то частная производная вектора р является вектором, компоненты которого суть частные производные его компонентов:
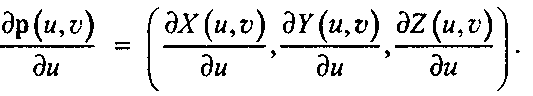
(6.26)В дальнейшем мы будем применять эти формулы ко всем типам исследуемых поверхностей.
Нормальный вектор к поверхности, заданной неявно Для поверхности, заданной в неявной форме, F(x, у, z) = О, применяется другое выражение. Нормальное направление в точке (х, у, z) поверхности может быть найдено с помощью градиента (gradient) от F, который обозначается VF и определяется следующим образом [Thomas, 53]:
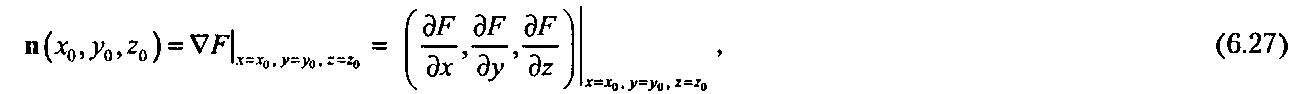
где каждая частная производная вычислена в нужной точке (х0, уа, г0). Если точка (х0, уа, 20) исследуемой поверхности соответствует точке Р(и0, у0) ее параметрической формы, то вектор п(ха, уа, га) имеет то же направление, что и вектор п(м0, &0) в уравнении (6.25), однако их длины могут различаться. Однако при желании его также можно нормировать.
Пример 6.5.2. Снова плоскость
Рассмотрим еще раз плоскость с нормалью п, проходящей через точку А. Пусть уравнение этой плоскости задано неявно выражением Р(х, у,г) = п- ((х, у, г) - А) = 0 или в виде: пхх + пуу + пг - п А = 0. Эта плоскость, как и следовало ожидать, имеет градиент = п.
Отметим, что в формуле для нормального вектора, использующей градиент, нормаль рассматривается как функция от х, у, г, а не от и, V. Иногда нам известны для поверхности сразу ее внешне-внутренняя функция Р(х,у, г) и параметрическая форма р(и, и) = Х(и, V)! + У(и, V)'} + 2{и, v)k. В таких случаях параметрическую форму нормального вектора п(ы, V) в точке (и, V) проще всего найти в два этапа:
1. Нормаль в точке (х, у, г) выразить из уравнения (6.27) через х, у, г.
