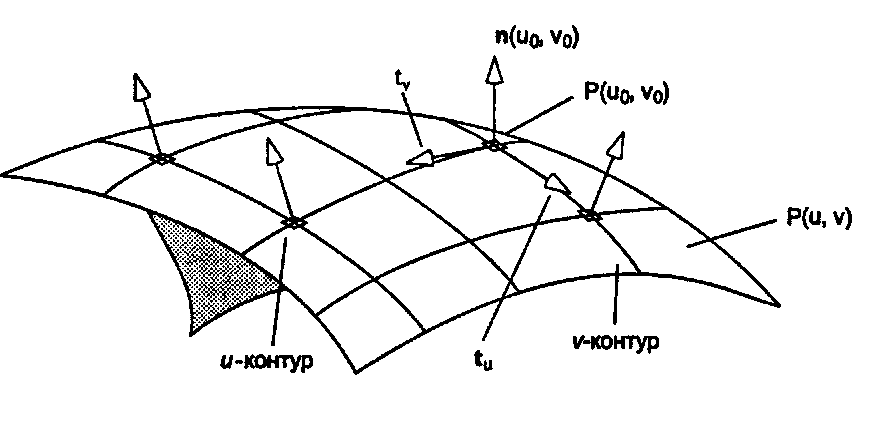
Рис 6.45. Нормальный вектор к поверхности Чтобы определить направление, нормальное к поверхности в лежащей на ней точке Р(и0, v0), нужно рассмотреть малую часть поверхности вокруг этой точки. Если эта область достаточно мала и поверхность в окрестности точки изменяется «плавно», то данная область будет почти плоской. Следовательно, она локально ведет себя как маленький плоский фрагмент, у которого имеется вполне определенное нормальное направление. На рис. 6.45 показана часть поверхности с нарисованными в различных точках нормальными векторами. Видно, что направление нормального вектора в различных точках поверхности также различно.
Обозначим п(ы, v) нормаль в точке при данных значениях параметров (и, v). Рассмотрим теперь, как ее можно вычислить.
Нормальный вектор к поверхности, заданной параметрически Как и следовало ожидать, вектор п(ы0, v0) имеет форму векторного произведения двух векторов, лежащих на малой плоской части в окрестности точки (ы0, v0). Будучи векторным произведением, он заведомо перпендикулярен к обоим векторам. Эти два вектора на плоскости (на рис. 6.45 они обозначены как tu и tc) являются касательными к ней векторами. В дальнейшем мы увидим, что они связаны с частными производными вектора р(ы, v) (это вектор от начала координат до точки Р(и, v) на поверхности)1, вычисленными в искомой точке [Thomas, 194]. Следовательно, выражение для нормального вектора имеет вид"images/tmp8E4A-409.png">
(6.25)1 Поскольку вектор р(и, V) является разностью Р(и, с) - (О,0,0), то частная производная от р() будет такая же, как от Р().
6.5. Каркасные аппроксимации гладких объектов где вертикальная черта означает, что производные' вычислены при и = и0 и V = г>0. Полученный таким способом вектор п(ид, иа) не является единичным вектором автоматически, однако при желании его можно нормировать.
Пример 6.5.1. Применимо ли уравнение (6.25) к случаю плоскости?
Рассмотрим плоскость, заданную параметрически: Р(и, V) = С + аи + Ъь. Частная производная Р по и равна вектору а, а по V - вектору Ь. Тогда, в соответствии с равенством (6.25), п(и, V) = а х Ь; нетрудно видеть, что этот результат правильный.
