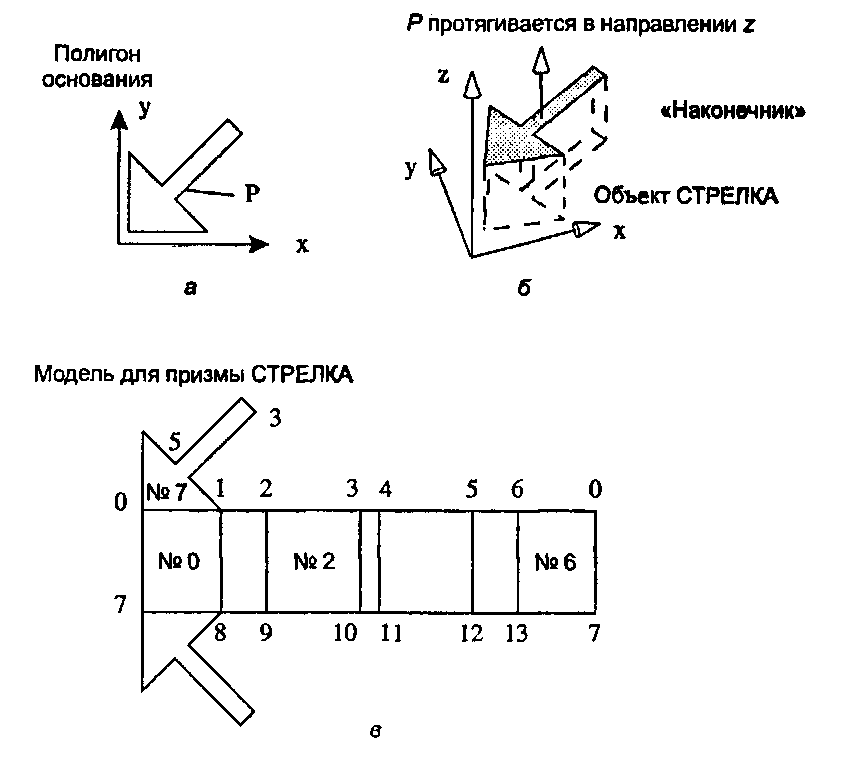
Рис. 6.30. Пример призмы: а) полигон основания; б) Р заметается в направлении г; в) модель для призмы СТРЕЛКА
Моделирование поверхностей полигональными сетками
Как выглядит список граней, описывающий призму СТРЕЛКА? Эту призму можно «развернуть» в модель, показанную на рис. 6.30, в, чтобы были видны все ее девять наружных граней. Призма имеет семь прямоугольных боковых граней, а также основание (base) Р и крышку (cap). Например, грань 2 определяется вершинами 2, 9,10,3.
Поскольку данная призма имеет плоские грани, мы связываем с каждой вершиной грани один и тот же нормальный вектор, то есть нормальный вектор к самой грани.
Для малого бизнеса аутсорсинг-ИТ услуг тут.
Построение сетки для призмы
Желательно иметь инструмент, создающий сетку для призмы на основе произвольного полигона. Пусть основанием призмы является полигон с Nвершинами (xiyyt). Занумеруем вершины основания числами 0,…, N- 1, а вершины крышки числами N,…, 2N- 1, так чтобы ребро соединяло вершины с номерами і иі + N, как показано на рис. 6.33. В этом случае список вершин строится просто и содержит точки (*., ур 0) и (х.,yt, Н) для і - 0,1,…,N- 1.
Список граней построить также несложно. Запишем вначале «боковые» грани, или «стены», а затем добавим основание и крышку. Для j-й стенки (/ - 0,…, N - 1) создадим грань с четырьмя вершинами, имеющими индексы j, j + N, next(j') + N, next(j), где next(j') - j + 1, за исключением j, равного N- 1, для которого next(j) - 0. Это условие обеспечивает «циклический возврат» от (N - 1)-й вершины к нулевой. Тогда имеем: или, на языке программного кода, next - (j < (N-D) ? (j + 1) : 0. Каждая грань добавляется в список граней по мере ее создания. Нормальный вектор к каждой грани легко находится методом Ньюэлла, описанным ранее. Затем мы создаем основание и крышку и добавляем их в список граней. Более подробно о создании каркасных моделей для призм рассказывается в тематическом задании 6.3.
6.4.2. Совокупности экструзивных призм: «кирпичная кладка»
