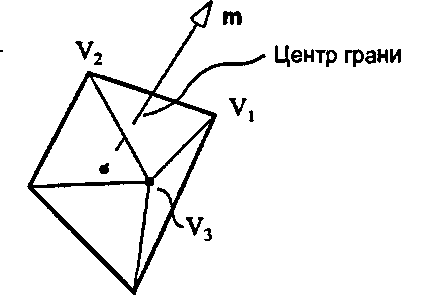
Тетраэдр
Список вершин тетраэдра зависит, разумеется, от положения тетраэдра, его ориентации и размера. Интересно, что тетраэдр можно вписать в куб (так, что четыре его вершины располагаются в углах куба, а четыре его ребра лежат на гранях куба). Рассмотрим единичный куб с вершинами (±1, ±1, ±1) и выберем тетраэдр так, чтобы одна его вершина находилась в точке (1,1,1). Тогда этот тетраэдр будет описываться списками вершин и граней, приведенными в табл. 6.5 [ВИпп, 30].
Таблица 6.5. Список вершин и список граней для тетраэдра
|
Список вершин |
Список граней |
|||
|
Вершина х |
У |
г |
Номер грани |
Вершины |
| 0 1 | 1,2,3 | |||
| 1 1 | -1 | -1 | 0,3,2 | |
| 2 1 | -1 | 0,1,3 | ||
| 3 -1 | -1 | 0,2,1 |
Икосаэдр
Список вершин икосаэдра более сложен, однако его можно упростить, если использовать одно замечательное обстоятельство. Рисунок 6.21 показывает вписанные в икосаэдр три взаимно перпендикулярных золотых прямоугольника, поэтому список вершин икосаэдра можно непосредственно прочитать с этого рисунка. Совместим каждый золотой прямоугольник с одной из координатных осей. Для удобства масштабируем эти прямоугольники так, чтобы их длинные ребра простирались от -1 до 1 вдоль соответствующих осей. Тогда короткое ребро каждого прямоугольника будет находиться в пределах от -г до т, где г = (>/5-1у2 - 0,618… - величина, обратная золотому отношению ф. Отсюда легко получить координаты вершин для списка, который приведен в табл. 6.6.
Моделирование поверхностей полигональными сетками
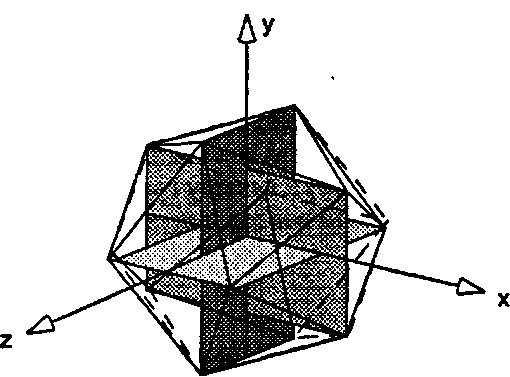
Рис. 6.21. Золотые прямоугольники, определяющие икосаэдр Таблица 6.6. Список вершин для икосаэдра
|
Вершина |
x |
у |
г |
|
г |
|||
|
-г |
|||
|
г |
|||
|
-г |
|||
| -1 |
-г |
||
| -1 |
г |
||
|
г |
|||
|
-г |
|||
|
г |
-1 | ||
|
-г |
-1 | ||
| -1 |
г |
||
| -1 |
-г |
На рис. 6.22 приведена модель икосаэдра. С этого рисунка можно непосредственно считывать список граней для икосаэдра. (Вопрос"images/tmp8E4A-378.png" alt="Модель икосаэдра">
Рис. 6.22. Модель икосаэдра
6.3. Многогранники Иногда предпочитают слегка изменить модель для икосаэдра, приведя ее к форме, показанной на рис. 6.23. Такая форма проясняет тот факт, что икосаэдр состоит из антипризмы (на рисунке она закрашена) и двух пятиугольных пирамид в его вершине и основании.
