Рассмотрим двойственную пару куб - октаэдр. Грань 4 куба окружена вершинами 1,5,6,2. Тогда из двойственности следует, что вершина 4 октаэдра окружена гранями 1, 5, 6, 2. Отметим, что поскольку тетраэдр является двойственным самому себе, то для него список вершин, окружающих k-ю грань, совпадает со списком граней, окружающих k-ю вершину.
1 Названо по имени швейцарского математика Л. Шлефли (L. Schlafli, 1814-1895).
Моделирование поверхностей полигональными сетками
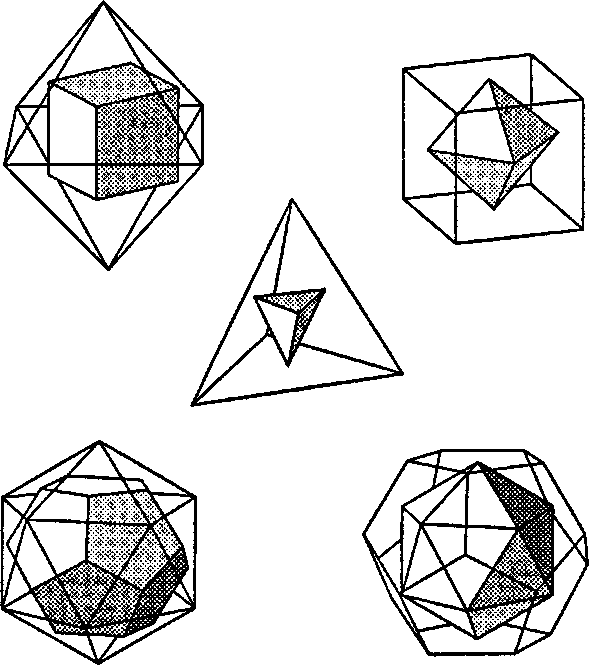
Рис. 6.18. Двойственные Платоновы тела
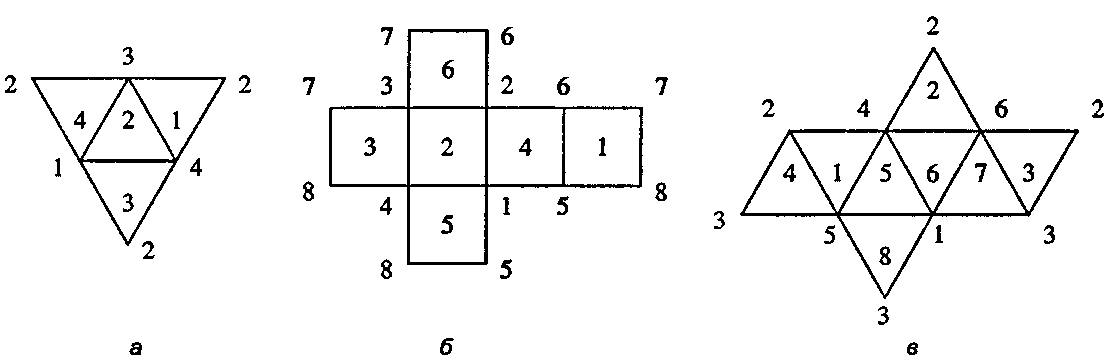
Рис. 6.19. Развертки: а) тетраэдр; б) куб; в) октаэдр
Вершина 4 октаэдра является центром грани 4 куба. Напомним из главы 4, что координаты центра грани вычисляются как среднее арифметическое координат всех вершин, принадлежащих этой грани. Следовательно, если нам известны вершины V,, У5, У6, У2 для грани 4 куба, то мы сразу же получим:
(6.3)Практические упражнения
6.3.7. Октаэдр
Рассмотрим октаэдр, являющийся двойственным телом для куба. Постройте списки вершин и граней для октаэдра.
6.3.8. Проверка двойственности Исходя из списков граней и вершин октаэдра из предыдущего упражнения, найдите двойственный ему многогранник и убедитесь, что он является кубом.
6.3. Многогранники Нормальные векторы к Платоновым телам Если мы хотим построить сетки для Платоновых тел, то мы должны вычислить для каждой грани нормальный вектор. Это можно сделать обычным способом с использованием метода Ньюэлла, однако высокая степень симметричности Платоновых тел допускает гораздо более простой подход. Пусть тело центрировано относительно начала координат, тогда мы видим, что нормальный вектор к каждой грани - это вектор из начала координат (радиус-вектор) к центру грани, представляющему собой среднее значение вершин. На рис. 6.20 показан нормальный вектор для октаэдра; нормаль к грани равна просто т = -|-2-. (6.4)
(Заметим, что этот вектор совпадает с вектором, проведенным из начала координат к соответствующей вершине двойственного к данному Платонову телу.)
Рис. 6.20. Использование симметрии для нахождения нормали к грани
