Итак, согласно данному определению, полиэдр представляет собой единый монолитный объект. Из этого следует, что: О каждое ребро принадлежит ровно двум граням; О в каждой вершине встречается не менее трех ребер; О грани не являются взаимопроникающими (interpenetrate): две грани или не имеют общих точек, или пересекаются только вдоль их общего ребра.
На рис. 6.8 объект ПИРАМИДА безусловно является полиэдром. Очевидно, что КОЛЬЦО ограничивает некоторое пространство, поэтому оно является полиэдром, но только если его грани плоские. Однако это не простой полиэдр, поскольку в нем имеется отверстие. Кроме того, две его грани сами содержат отверстия. Является ли полиэдром объект НЕВОЗМОЖНОЕ? Почему? Если не принимать во внимание текстуру граней, то САРАЙ можно смоделировать как два полиэдра - один для главного здания и второй для силосной башни.
отели Юар 5 звезд, отдых в ЮАР и туры.
Формула Эйлера Формула Эйлера (она легко доказывается; см., например, [Courant, 49]) устанавливает фундаментальное соотношение между количеством граней, ребер и вершин (соответственно F, Е, V) простого многогранника:
V+F-E-2.Например, для куба v= 8, F= 6, е= 12.
Моделирование поверхностей полигональными сетками
Обобщение этой формулы на непростой полиэдр [Foley, 64] выглядит так: V+F-E = 2 + H-2g,
(6.2)где Я - общее число отверстий, имеющихся в гранях, а С - число отверстий в самом полиэдре. На рис. 6.11,а изображен параллелепипед, содержащий отверстие в форме другого параллелепипеда. Две его торцевые грани выдвинуты из основного параллелепипеда. Для этого объекта V = 16, Е= 16, Е = 32, Я = О, С = 1. На рис. 6.11,6 изображен полиэдр с частично проникающим в него отверстием А и сквозным отверстием В. Здесь У= 24, ^= 15, Е = 36, Я = 3, С = 1. Обе совокупности величин удовлетворяют формуле Эйлера.
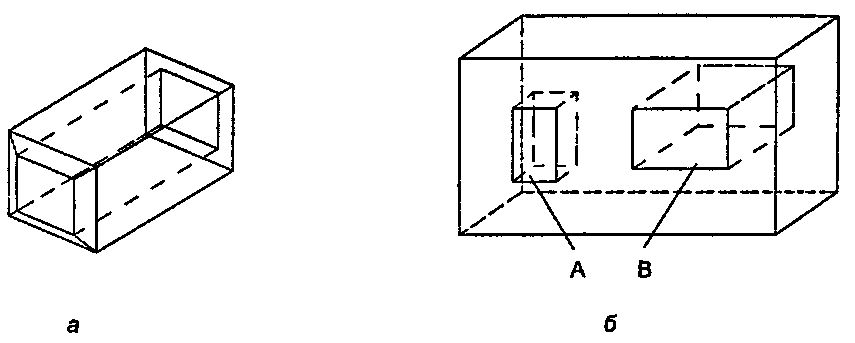
Рис. 6.11. Полиэдр с отверстиями
«Структуру» полиэдра удобно описывать с помощью диаграммы Шлегеля (Schlegel diagram), которая основана на взгляде на полиэдр из точки, расположенной на некотором расстоянии от центра одной из его граней, как предлагается на рис. 6.12, а. Такой способ рассмотрения куба приводит к диаграмме Шлегеля, приведенной на рис. 6.12, б. Передняя грань представляется как большой полигон, окружающий остальные грани.
