Рассмотрим четырехугольник, изображенный на рис. 6.5, с вершинами (0,0,0), (1,0,0), (0,0,1) и (1, а, 1). Если а отлично от нуля, то данный четырехугольник является неплоским полигоном. Найдите «нормаль» к этому полигону с помощью метода Ньюэлла и исследуйте, насколько хороша эта ее оценка для различных значений параметра а.
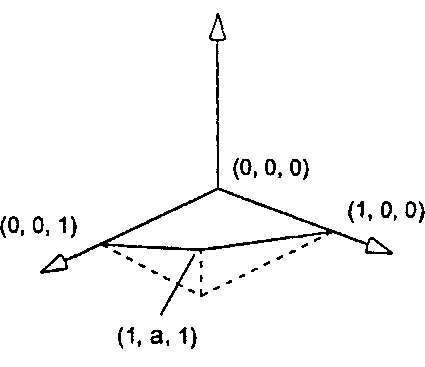
Рис. 6.5. Неплоскии полигон
6.2.3. Представление «базового куба» Составьте списки вершин, нормалей и граней для «базового куба» с центром в начале координат, ребра которого длиной в две единицы выровнены по координатным осям. В этом случае восемь его вершин располагаются в точках с восемью возможными комбинациями знаков «+» и «-» в списке (+1, ±1, ±1).
6.2.4. Грани с отверстиями На рис. 6.6 показано, каким образом можно записать в список грань, содержащую отверстие. Как видно из рисунка, нужно добавить пару фиктивных ребер, которые соединяют разрыв между контуром грани и отверстием.
Обход грани производится так (если двигаться по внешней поверхности), что «внутренность» грани располагается слева. Тогда отверстие обходится по часовой стрелке. Предполагая, что мы смотрим на грань с ее внешней стороны, получим следующий список вершин"images/tmp8E4A-362.png" alt="Грань, содержащая отверстие">
Рис. 6.6. Грань, содержащая отверстие
6.2.3. Свойства сеток Имея сетку, заданную списками вершин, нормалей и граней, мы можем поинтересоваться, что за объект представляет эта сетка. Вот некоторые любопытные свойства сетки.
О Монолитность (Solidity). Как уже упоминалось, сетка представляет монолитный объект, если совокупность его граней заключает в себе некоторое конечное пространство.
О Связность (Connectedness). Сетка называется связной, если между любыми двумя вершинами существует непрерывный путь вдоль ребер полигона. (Если сетка не является связной, то обычно она представляет более одного объекта.)
