Пусть (с, сі, 1 )г - представление точки Рв новой системе № 2. Чему равны значения а и Ь в представлении (а, Ь, 1)гэтой же точки Р в исходной системе № 1? Для ответа на этот вопрос достаточно умножить М (слева) на (с, й, 1)г:
иглоукалывание в Москве форум отзывы.
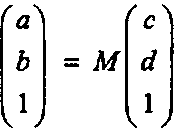
5.4. Изменения систем координат
Обобщая эти рассуждения, сформулируем следующую «теорему». Предположим, что система координат № 2 получена из системы координат № 1 посредством аффинного преобразования М. Предположим далее, что (Рх, Р , 1) - это координаты точки Р в системе координат № 2. Тогда координаты точки Р в системе № 1 равны МР.
Данная «теорема» может показаться некоторым читателям слишком очевидной, но для тех, кто с этим не согласен, ее доказательство рассматривается в упражнениях в конце раздела. Разумеется, этот результат справедлив и для трехмерных систем, и мы будем широко использовать его при вычислении преобразования трехмерных точек, когда они проходят через графический «конвейер».
Пример 5.4.1. Поворот системы координат
Вновь рассмотрим преобразование из примера 5.2.5, где осуществляется поворот точек на 30° относительно точки (-2,3) (см. рис. 5.22, б.) Это преобразование отображает начало отсчета Ь и оси і и j в систему № 2, как показано на рисунке. Рассмотрим теперь точку Р с координатами (Рх, Р, 1)г в новой системе координат. Чему равны координаты этой точки в системе координат № 1? Ответ прост: МР. Например, точка (1,2,1)г в новой системе соответствует точке М(1,2,1)г - (1,098,3,634,1)г в исходной системе. (Нарисуйте это на бумаге.) Отметим, что точка (-2,3,1)г- центр вращения данного преобразования - является неподвижной точкой преобразования: М(-2,3,1)г- (-2,3,1)г. Поэтому, если мы возьмем точку Р - (-2,3,1)гв новой системе, то она представляется в новой системе тоже как (-2,3,1)г. (Проверьте это графически.)
Последовательные изменения координатного фрейма Рассмотрим теперь формирование преобразования, состоящего из двух последовательных изменений системы координат. Каков будет суммарный эффект? Как показано на рис. 5.32, система № 1 переходит в систему № 2 посредством преобразования Т{(.), а система № 2 трансформируется затем в систему № 3 посредством преобразования Т2(.). Отметим, что система № 3 трансформируется относительно № 2.
