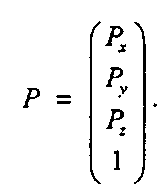
Пусть теперь Т( ) является аффинным преобразованием, которое преобразует точку Р в точку (). Тогда, аналогично случаю двух измерений, преобразование Т( ) отображается матрицей М, размерность которой теперь равна 4 на 4, а именно:
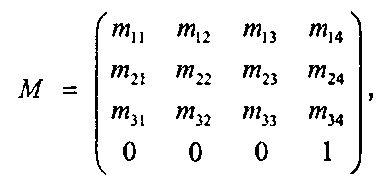
(5.23)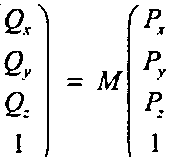
поэтому можно сказать, что отображение точки <2 можно найти, умножив точку Р (справа) на матрицу М:
(5.24)Отметим еще раз, что последняя строка матрицы аффинного преобразования состоит из ряда нулей, заканчивающегося одной единицей. (Это уже не будет выполняться, когда мы перейдем к проективным матрицам в главе 7.)
5.3.1. Элементарные трехмерные преобразования В этом разделе мы рассмотрим природу каждого из элементарных трехмерных преобразований, после чего составим из них трехмерные аффинные преобразования общего вида.
10 Ф. Хилл
Преобразования объектов
Перемещение В случае чистого перемещения матрица М имеет простую форму:
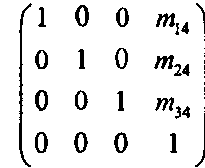
Проверьте, что 0, ~ МР означает простое смещение точки 0, на вектор ш = (ты, т2А, тм).
Масштабирование Трехмерное масштабирование является прямым расширением двумерного и его матрица равна:
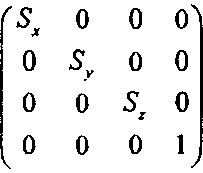
(5.25)где три константы 5Х, 5у и 5г определяют масштабирование по соответствующим координатам. Как и в двумерном случае, масштабирование производится относительно начала отсчета. На рис. 5.24 показан эффект масштабирования в 2-направлении с множителем 0,5 и в ^-направлении с множителем 2. Отметим, что на рисунке показаны различные прямые до и после преобразования; здесь используется то важное обстоятельство, что прямые преобразуются в прямые.
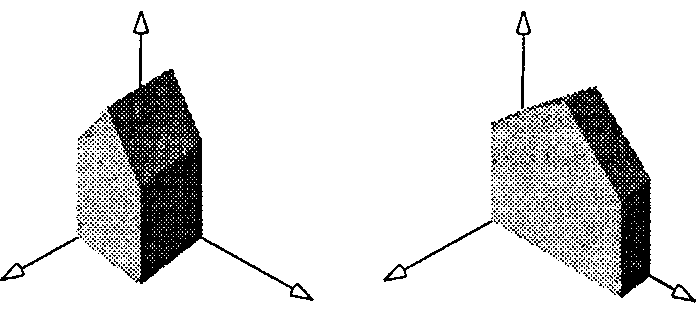
Рис. 5.24. Масштабирование базового сарая Сдвиг
Трехмерные сдвиги отличаются большим разнообразием, чем их двумерные аналоги. Матрица простейшего элементарного сдвига является единичной матрицей, в которой один нуль заменен некоторой величиной /"images/tmp8E4A-296.png">
(5.26)Отсюда Q = (Рх,/Рх+ Ру, Р2); то есть Ру смещено на некоторую величину, пропорциональную Рх, а остальные компоненты остались неизменными. Это вызывает эффект, подобный показанному на рис. 5.15 для двумерного случая. Голдманом [Goldman, 84] рассмотрен намного более общий случай трехмерного сдвига, который мы будем рассматривать в тематическом задании 5.4.
