5.2.13. Отражение относительно прямой х = у
Докажите, что отражение относительно прямой х = у эквивалентно отражению относительно х и последующему повороту на 90°.
5.2.14. Масштабирование относительно произвольной точки Сформируйте аффинное преобразование, которое масштабирует точки относительно опорной точки ( Ух, Уу). Проверьте суммарное преобразование на нескольких точках, чтобы убедиться в правильности работы операции масштабирования. Сравните это преобразование с преобразованием поворота относительно опорной точки.
5.2.15. Сдвиг относительно наклонной оси Сформируйте преобразование, которое сдвигает точку вдоль оси, описываемой вектором и, наклоненным на угол 8, как показано на рис. 5.19. Точка Р сдвигается вдоль вектора и на величину, являющуюся частью /расстояния а1 между точкой Р и указанной осью.
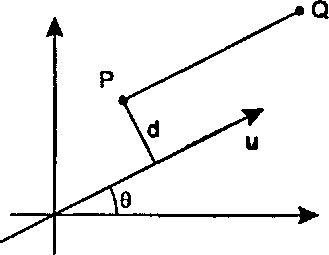
Рис. 5.19. Сдвиг вдоль наклонной оси 5.2.16. Преобразование трех точек Любое аффинное преобразование полностью определяется указанием того, что оно делает с тремя точками. Для иллюстрации этого утверждения найдите аффинное преобразование, которое превращает треугольник С с вершинами (-3, 3), (0,3) и (0,5) в равносторонний треугольник £) с вершинами (0,0), (2,0) и (1, л/З ), как показано на рис. 5.20. Для решения этой задачи используйте следующую последовательность трех элементарных преобразований.
1. Переместить точку С вниз на 3 и вправо на 3, после чего вершина с превратится в с'.
2. Масштабировать по х в 2/3 раз и по у в -Уз/2 раз, чтобы треугольник Б совпал с треугольником С по ширине и по высоте.
3. Осуществить сдвиг на -\I-Jb в направлении х, чтобы верхняя вершина треугольника С совпала с соответствующей вершиной треугольника О.
5.2. Введение в преобразования
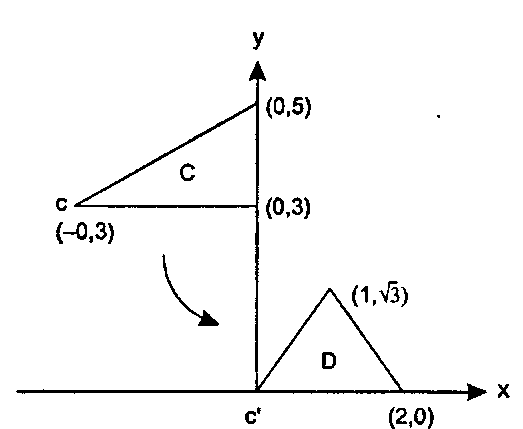
Рис 5.20. Превращение одного треугольника в другой Убедитесь, что данное преобразование действительно преобразует треугольник С в треугольник D. Теперь найдите преобразование, обратное к этому, и покажите, что оно превращает треугольник D обратно в треугольник С.
5.2.17. Неподвижные точки аффинного преобразования
