5.2. Введение в преобразования Р « (i?cos(0), i?sin(0)). Точка Q должна отстоять от начала координат на такое же расстояние, что и Р, но под углом 0 + ф (к оси ОХ). После тригонометрических преобразований получим, что координаты точки Q равны:
Q- Дсоз(0 + 0), (^-Дап(в + 0).
Подставим в это уравнение два известных тригонометрических соотношения:
COS(0 + 0) - COS(0)COS(0) - Sin(0)sin(0), Sin(0 + 0) - sin(0)cos(0) + cos(0)sin(0)и после замены Px~ #cos(0) и Py = #sin(0) получим уравнение (5.9).
Практическое упражнение 5.2.3. Поверните точку
Примените уравнение (5.9) для нахождения образа каждой из следующих точек после поворота относительно начала отсчета: а) (2,3) на угол -45°; б) (1,1) на угол-180°; в) (60,61) на угол 4°.
В каждом случае проверьте результат на миллиметровке и численно сравните расстояния исходной точки и ее образа от начала отсчета. Решение а) (3,5355,0,7071); б) (-1,-1); в) (55,5987, 65,0368).
Сдвиг На рис. 5.15 приведен пример сдвига «в х-направлении» (или «вдоль х>). В этом случае координата у каждой точки остается неизменной, а каждая координата х перемещается на величину, которая линейно возрастает с ростом у. Сдвиг в х-направлении описывается следующими формулами:
Q-P+hP,Q =Р, где коэффициент h определяет, какая доля координаты у точки Р должна быть добавлена к координате х. Значение h может быть положительным или отрицательным. Матрица, соответствующая такому типу сдвига, имеет вид:
( \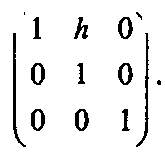
(5.11)Сдвиг иногда используют для создания курсивных (italic) букв из стандартных (regular). Можно осуществлять сдвиг «вдоль у», для которого Рх и Qy" gPx+ Ру для некоторой величины g, в таком случае матрица преобразования имеет вид:
(5.12)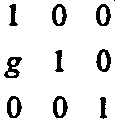
Преобразования объ'ектов
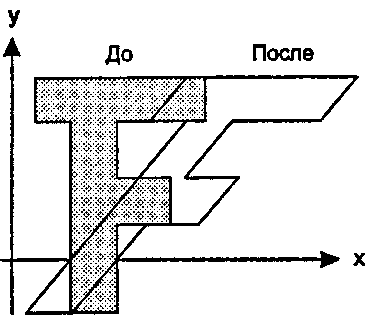
Рис. 5.15. Пример сдвига Пример 5.2.2
В какую точку произойдет сдвиг точки (3,4), если в уравнении (5.11) А = 0,3? Решение
(2 =(3 +(0,3)4,4)-(4,2,4). Пример 5.2.3
Пусть в уравнении (5.12) g = 0,2. В какую точку отображается точка (6, -2)? Решение
