Практическое упражнение
5.2.2. Нарисуйте эффект масштабирования Аффинное преобразование, состоящее из чистого масштабирования, использует масштабные множители Sx= 3 и Sy = -2. Определите и нарисуйте изображения каждого из трех объектов, показанных на рис. 5.12, после такого преобразования. (Используйте то обстоятельство (оно будет проверено позже), что аффинные преобразования переводят прямые линии в прямые линии, а эллипсы - в эллипсы.)
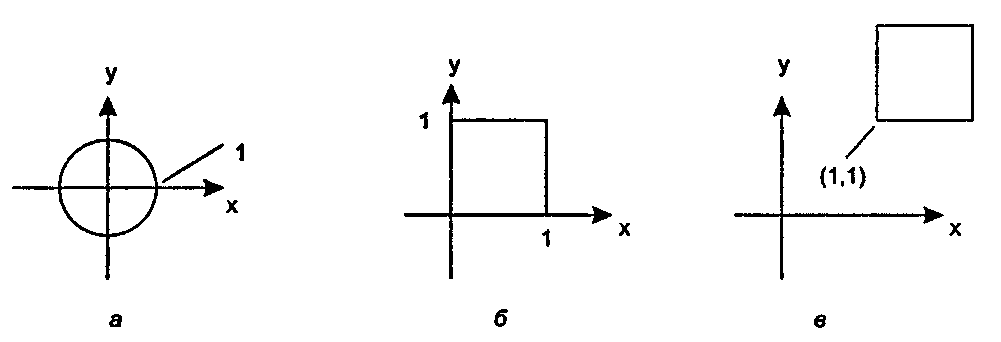
Рис 5.12. Объекты для масштабирования Поворот
Одной из основных операций в графике является поворот изображения относительно заданной точки на некоторый угол. На рис. 5.13 показано множество точек, которое поворачивается относительно начала отсчета на угол 9 - 60°.
В том случае, когда Т( ) является поворотом относительно начала отсчета, вектор перемещения d равен нулю и уравнение (I = Т(Р) имеет следующий вид"images/tmp8E4A-265.png">
Преобразования объектов
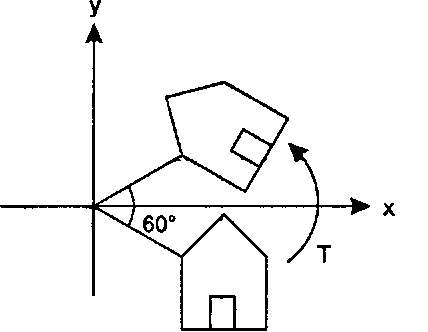
Рис. 5.13. Поворот точек на угол 60° Как будет показано ниже, при положительных значениях угла 0 поворот осуществляется против часовой стрелки (CCW rotation). В матричной форме чистый поворот относительно начала отсчета имеет вид"images/tmp8E4A-267.png">
Пример 5.2.1
Найти преобразованную точку Q полученную при повороте точки Р - (3,5) относительно начала отсчета на угол 60°. Решение Для угла 60° cos(0) = 0,5 и sin(0) - 0,866, тогда из уравнения (5.9) следует Qx- (3)(0,5) - (5)(0,866) - -2,83
а- (3)(0,866) + (5)(0,5) - 5,098.
Проверьте полученный результат на миллиметровке, для чего проведите из точки (3, 5) дугу в 60° и прочитайте координаты отображенной точки. Кроме того, проверьте численно, что точки (2 и Р находятся на одинаковом расстоянии от начала отсчета. (Чему равно это расстояние?)
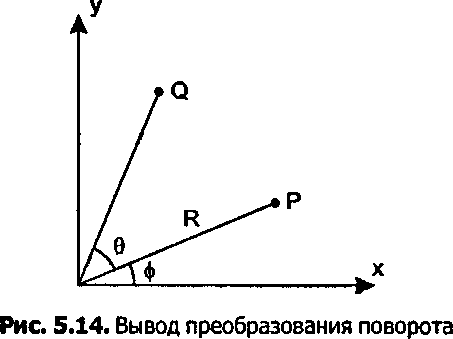
Вывод преобразования поворота Мы хотим продемонстрировать, что уравнение (5.9) верно. На рис. 5.14 показано, как найти координаты точки 0, полученной в результате поворота точки Р относительно начала отсчета на угол 0. Если точка Р находится на расстоянии Я от начала отсчета под некоторым углом ф (к оси ОХ), то
