Дж. М. Бэрри (]. М. Вате)
Аффинные преобразования наиболее часто используются в компьютерной графике. Помимо всего прочего, они упрощают масштабирование, поворот и перестановку изображений. Последовательность аффинных преобразований легко может быть преобразована в простое суммарное аффинное преобразование; кроме того, аффинные преобразования допускают компактное матричное представление.
Форма аффинных преобразований проста: координаты точки (2 являются линейными комбинациями соответствующих координат точки Р. В матричной записи это выглядит так:

где тп, тп,… - шесть известных констант. Компонент 0^ состоит из долей Рх и Ру, то же касается и 0^. Такое «перекрестное опыление» компонентов XVI у вызывает повороты и сдвиги.
Аффинное преобразование равенства (5.3) имеет удобное матричное представление, которое помогает уяснить суть дела1:
(5.4)Непосредственное перемножение членов правой части этого равенства показывает, что оно совпадает с равенством (5.3). В частности, отметим, что третья строка матрицы обеспечивает равенство едини-
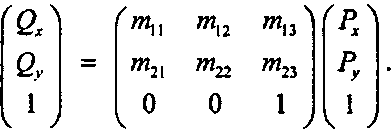
Обзор матриц дан в приложении 2.
5.2. Введение в преобразования це третьему компоненту Ск Для любого аффинного преобразования третья строка матрицы всегда равняется (0,0, 1).
Векторы могут быть преобразованы так же, как и точки. Напомним, что если координаты вектора V равны V. и V, то его представление в координатах фрейма является вектором-столбцом с нулевым третьим компонентом. Действие на вектор того же аффинного преобразования, какое применялось в равенстве (5.4) для точек, имеет следующий вид:
(5.5)причем ясно, что исходный вектор превращается в другой вектор: его третий компонент всегда равен нулю.
Практическое упражнение
5.2.1. Применить преобразование Аффинное преобразование задано следующей матрицей:
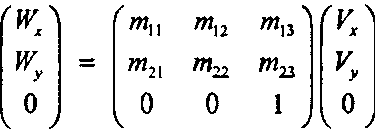
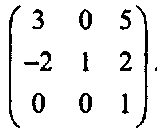
Найдите образ 0, точки Р - (1,2). Решение
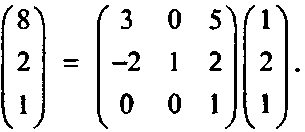
5.2.3. Геометрические эффекты элементарных двумерных аффинных преобразований Аффинные преобразования осуществляют комбинации из четырех элементарных преобразований: перемещение, масштабирование, поворот и сдвиг.
