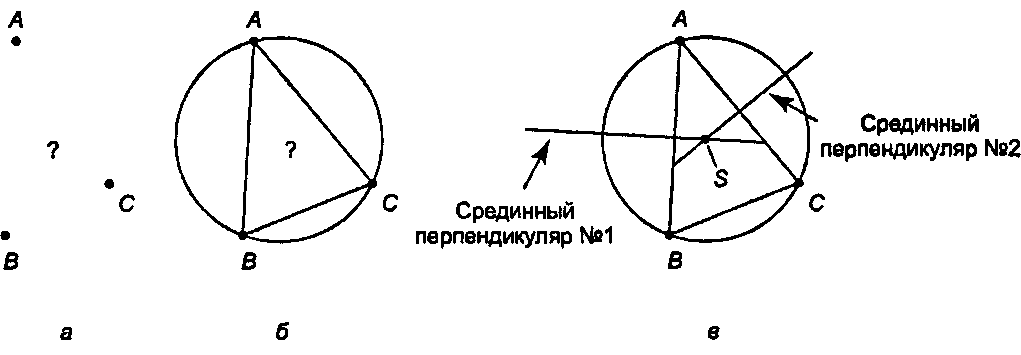
Рис. 4.34. Нахождение описанной окружности: а) какая окружность? б) она выглядит так; в) так находится ее центр
Рисунок 4.35, е показывает, как найти описанную окружность. Центр 5 искомой окружности должен быть равноудален от всех трех вершин, поэтому он должен располагаться на срединном перпендикуляре (perpendicular bisector) каждой из сторон треугольника ABC (срединный перпендикуляр - это множество всех точек, равноудаленных от двух заданных точек). Таким образом, мы можем определить центр окружности 5, если вычислим точку пересечения двух срединных перпендикуляров.
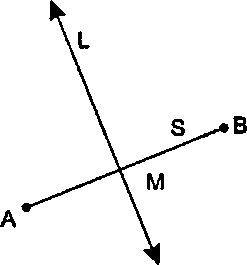
Рис. 4.35. Срединный перпендикуляр для отрезка прямой Вначале покажем, как найти параметрическое представление срединного перпендикуляра для отрезка прямой. На рис. 4.35 показан отрезок 5 с концевыми точками АпВ. Его срединный перпендикуляр Ь является бесконечной прямой, которая проходит через середину М отрезка 5 перпендикулярно
4.6. Определение точки пересечения двух отрезков прямой к нему. Однако нам известно, что средняя точка Мопределяется выражением (А + В)/2 и что направление нормали задается выражением (В - А)1, поэтому параметрическая форма срединного перпендикуляра имеет вид"opengl1_264.html">⇐ Предыдущая| |Следующая ⇒
