Пример 4.5.10. Построение лоскута Пусть С - (1, 3, 2), а - (1,1, 0), b - (1,4, 2). Найдите углы плоского лоскута. Решение Из формул (4.48) получим четыре угла Р(0,0) - (1, 3,2), Р(0,1) = (2,7,4), Р(1,0) - (2,4,2), Р(1,1) - (3,8,4). Пример 4.5.11. Описание лоскута Найдите значения векторов a, b и точки С, образующие квадратный лоскут со стороной 4, с центром в начале отсчета и параллельную плоскости х, г.
4.6. Определение точки пересечения двух отрезков прямой Решение Углы этого лоскута равны соответственно (2,0,2), (2, 0, -2), (-2,0, 2) и (-2, 0, -2). В качестве точки С выбираем любой угол, например (2,0, -2). Тогда каждый из векторов а и Ь имеет длину 4 и параллелен одной из осей х или г. Выбираем в качестве вектора а = (-4,0,0), а в качестве вектора Ь = (0,0,4).
Практическое упражнение 4.5.9. Нахождение лоскута Найдите точку С и векторы а и Ь, образующие лоскут, четыре угла которого равны соответственно (-4,2,1), (1,7,4), (-2, -2,2) и (3,3,5).
4.6. Определение точки пересечения двух отрезков прямой Часто возникает необходимость вычислить точку, в которой пересекаются два отрезка прямой в двумерном пространстве (то есть на плоскости). Иногда такое вычисление необходимо для решения другой, связанной с этой задачи, например, чтобы выяснить, является ли полигон простым. Определение точки пересечения двух отрезков иллюстрирует мощность параметрического представления отрезков и скалярного произведения.
Задача: даны два отрезка прямой; требуется определить, пересекаются ли они, и если пересекаются, то найти точку их пересечения.
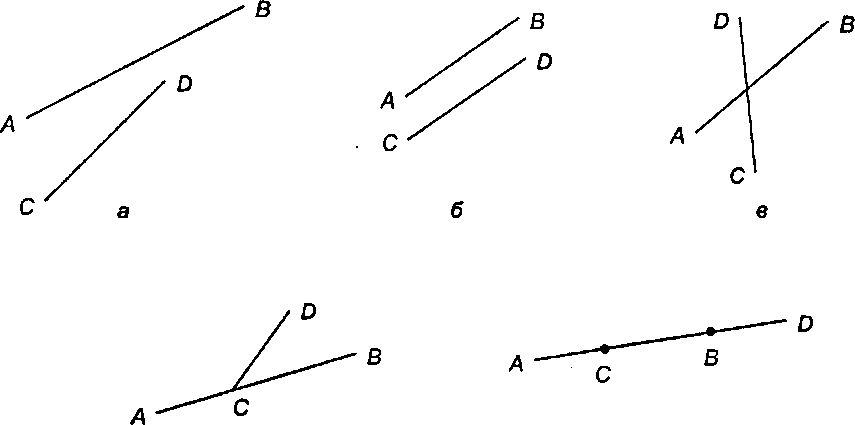
г д Рис. 4.33. Различные случаи для двух отрезков прямой Решение. Пусть один отрезок имеет концевые точки А и В, а другой - концевые точки С и D. Как показано на рис. 4.33, два эти отрезка могут быть расположены различными способами: они могут вовсе не пересекаться (рисунки а и б), иметь одну общую точку (в и г) или даже перекрываться в некоторой области (е). Они могут быть или не быть параллельны. Требуется единый подход, охватывающий все эти случаи.
Каждый отрезок имеет порождающую прямую (parent line) - бесконечную прямую линию, частью которой он является. Если две порождающие прямые не параллельны, то они пересекаются в некоторой точке. Вначале определим эту точку.
