Иногда удобнее преобразовать параметрическую форму к виду, где ее «компоненты» будут явными. Мы можем сделать это путем расписывания уравнения (4.43) по проекциям:

P(s, 0 = (Сх + as + bt, С + as + bt, Сг + as + bt). (4.44)

Можно также переписать параметрическую форму в уравнении (4.43) в явном виде в терминах заданных точек А, В к С. Используем определения векторов а и b для получения

P(s, t) = C + s(A-C) + t(B- Q,

что может быть перегруппировано в аффинную комбинацию точек:

P(s,t) = sA + tB + (l-s-t)C. (4.45)

Пример 4.5.6. Нахождение параметрической формы по трем точкам плоскости Рассмотрим плоскость, проходящую через точки А = (3,3,3), В = (5,5,7) и С= (1,2,4). Из равенства (4.43) следует, что данная плоскость имеет параметрическую форму P(s, t) = (1,2,4) + (2,1, -l)s + (4,3,3)t. Это равенство можно перегруппировать в компонентную форму: P(s, t) = (1 + 2s + 4t)i + (2 + s + 3t)j + + (4 - s + 3t)k или в аффинную комбинацию P(s, t) =5(3,3,3) +1(5,5,7) + (1 - s - 0(1,2,4).

Точечная нормальная форма для плоскости Плоскости также могут быть представлены в точечной нормальной форме, откуда легко выводится классическое уравнение для плоскости.

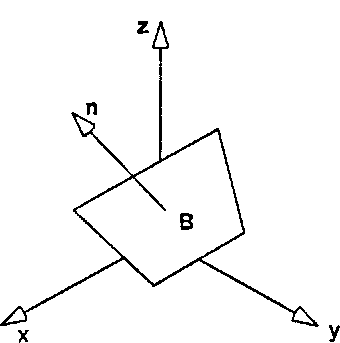
Рис. 4.30. Определение уравнения для плоскости

Векторные инструменты для графики

На рис. 4.30 показана часть плоскости Р в трех измерениях. Плоскость полностью определяется с помощью

О одной точки В - (Ьх, Ьу, Ьг), лежащей на ней. О направлением п - (пх, пу, пг), нормальным к этой плоскости. Подобно тому, как вектор, нормальный к прямой в двух измерениях, указывает ее направление, нормаль к плоскости указывает ориентацию этой плоскости в пространстве.

Известно, что нормаль п перпендикулярна любой прямой, расположенной в плоскости. Для произвольной точки Я = (х, у, г) плоскости вектор, проведенный из точки /? к точке В, должен быть перпендикулярен к нормали п, откуда п(Д-Я)-0. (4.46)

Это и есть точечное нормальное уравнение для плоскости. По форме оно идентично точечному нормальному уравнению для прямой"opengl1_256.html">⇐ Предыдущая| |Следующая ⇒