Уравнение (4.41) может быть записано с помощью скалярного произведения: (f,g) (х, у) = 1. Таким образом, для каждой точки прямой указанное скалярное произведение должно быть постоянным. Мы рассмотрим геометрическую интерпретацию «вектора» (/, g) и попутно усовершенствуем точечную нормальную форму прямой. Эта форма очень полезна в таких задачах, как отсечение, удаление скрытых линий и трассировка лучей. Формально в точечной нормальной форме ничего не сказано о числе измерений: в двумерном пространстве точечную нормальную форму имеет прямая, а в трехмерном пространстве ее имеет плоскость.

Пусть нам известно, что прямая L проходит через точки Си В, как показано на рис. 4.27. Что такое точечная нормальная форма прямой I? Если мы найдем вектор п, перпендикулярный к L, то для любой

4.5. Отображение ключевых геометрических объектов точки R = (х, у), лежащей на прямой L, вектор R - С должен быть перпендикулярен к вектору п, поэтому для R справедливо следующее условие: п (R - С) = 0 (точечная нормальная форма). (4.42)

Это называется точечным нормальным (point normal) уравнением для прямой; оно выражает тот факт, что указанное скалярное произведение должно быть равно нулю для любой точки R, лежащей на прямой. Это должно выполняться для любой точки, расположенной на прямой, и любого вектора, нормального к этой прямой.

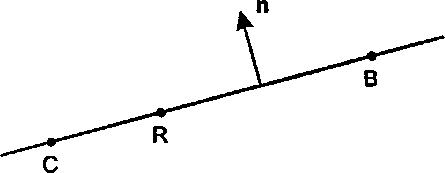
Рис. 4.27. Нахождение точечной нормальной формы для прямой Мы должны найти подходящий вектор п. Обозначим буквой Ь = В - С вектор, соединяющий точки С и В. Тогда вектор Ь1 (перп Ь) может служить в качестве искомого вектора п. Для построения точечной нормальной формы в качестве вектора п может выступать любое скалярное кратное от Ь1 (то есть любой вектор, полученный из Ь1 умножением на скаляр).

Пример 4.5.5. Найдите точечную нормальную форму

Пусть прямая L проходит через точки С = (3,4) и В = (5, -2). Тогда Ь = В - С = (2, -6) и Ъ1 = (6,2) (изобразите Ь1). В качестве точки, принадлежащей прямой, выберем С, тогда получим точечную нормальную форму"opengl1_253.html">⇐ Предыдущая| |Следующая ⇒