1 А именно в этой области программистам-графикам часто приходится туго: их программы создают такие изображения, которые выглядят хорошо в простых ситуациях, однако непостижимым образом становятся удивительно плохими, когда ситуация усложняется.

Векторные инструменты для графики

одна система координат (очень частое явление в графике) и когда происходит преобразование точки или вектора из одной системы в другую.

Обычно мы представляем себе систему координат как три оси, исходящие из начала отсчета, как было показано на рис. 4.2, б. Однако на самом деле система координат «расположена» где-нибудь «в мире» (in «the world») и ее оси лучше всего описываются тремя взаимно перпендикулярными векторами. В частности, важно явно задавать «местоположение» системы координат, поэтому мы расширяем понятие трехмерной системы координат1 до понятия трехмерного координатного «фрейма». Координатный фрейм (coordinate frame) состоит из заданной точки f>, называемой началом отсчета (origin), и трех взаимно перпендикулярных единичных векторов2: а, Ь и с.

На рис. 4.18 показан координатный фрейм, «находящийся» в некоторой точке Ь «в мире», с векторами а, Ь и с, изображенными так, что они исходят из точки Ь в качестве осей.

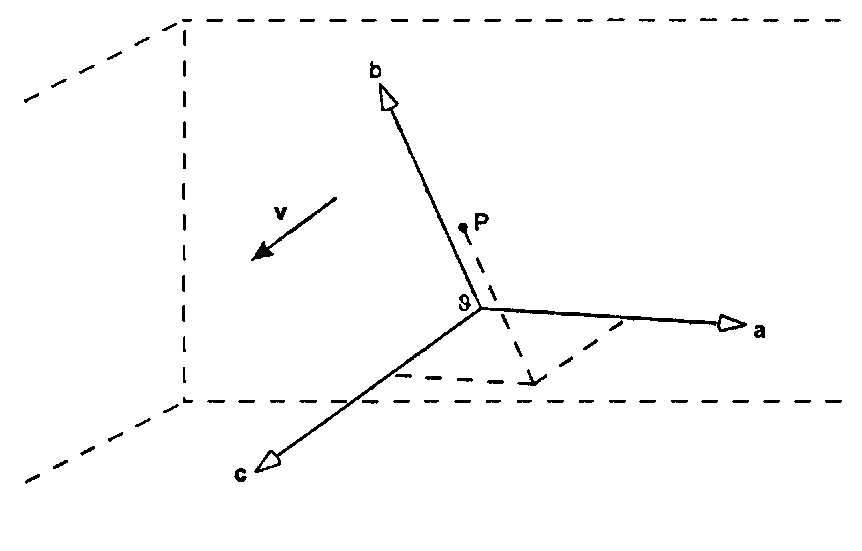
Рис. 4.18. Координатный фрейм, расположенный «в мире» Теперь для того, чтобы представить вектор V, мы должны найти такие три числа (о,, а2, v3), что

V = г),а + v2Ъ + ь3с, (4.32)

и сказать, что вектор V имеет в данной системе отображение (о,, ь2, а3).

С другой стороны, чтобы представить точку Р, мы рассматриваем ее местоположение как смещение на определенную величину относительно начала координат. Мы представляем вектор Р-Ь посредством нахождения трех чисел (р{,р2,р3) следующим образом"opengl1_240.html">⇐ Предыдущая| |Следующая ⇒