О Линейность: (а + b)1 = а1 + Ь\ и для любого скаляра А (Аа)1 = Ла1.

О а11 = (а1)1 -а (два перпа осуществляют реверсирование, то есть изменение направления на обратное).

4.3.6. «Перп-скалярное» произведение Любопытные вещи происходят при вычислении скалярного произведения перпа некоторого вектора на другой вектор, то есть а1 Ь. Назовем такую операцию «перп-скалярным произведением» («регр dot product») [Hill, 95]. Докажите, используя основное определение а1, что а1 b = aby - abx (величина перп-скалярного произведения), а1а = 0 (а1перпендикулярен к а),

|ai|2 = |a|2 (а1 и а имеют одинаковую длину), (4.21)

а1 b = -b1 а (а1 антисимметричен).

Векторные инструменты для графики

Четвертое утверждение означает, что перп-скалярное произведение является антисимметричным: перемещение знака 1 от одного вектора к другому изменяет знак скалярного произведения. Другие полезные свойства перп-скалярного произведения мы будем рассматривать по мере необходимости.

4.3.7. Вычисление перп-скалярного произведения Вычислите а Ь и ах Ь для векторов а - (3,4) и Ь - (2,1).

4.3.8. Определитель

Покажите, что а1 Ь можно записать в виде определителя

(Определения матриц и определителей приведены в приложении Б.) 4.3.9. Разные задачи О Докажите, что (а1 Ь)2 + (а Ь)2 - |а|2|Ь|2.

О Докажите, что если а + b + с - 0, то а1 b - bx с - с1 а.

4.3.5. Ортогональные проекции и расстояние от точки до прямой В графических приложениях часто возникают три геометрические задачи: проецирование (projecting) вектора на данный вектор, разложение (resolving) вектора на составляющие в одном и другом направлении, а также определение расстояния между точкой и прямой. Все эти три задачи упрощаются при использовании перп-вектора и перп-скалярного произведения.

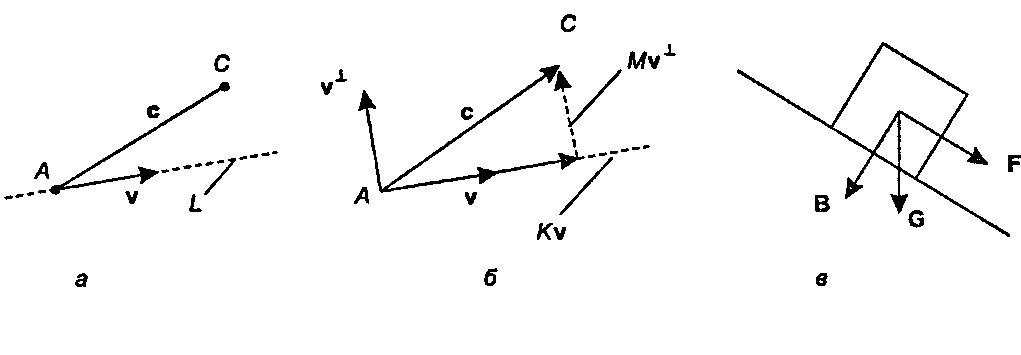
Рис. 4.13. Разложение вектора на два ортогональных вектора На рис. 4.13, а проиллюстрированы основные проблемы. Нам даны две точки Л и С, а также вектор v. Возникают следующие вопросы"opengl1_231.html">⇐ Предыдущая| |Следующая ⇒