Выпуклые комбинации векторов Выпуклые комбинации занимают важное место в математике и в многочисленных графических приложениях. Выпуклая комбинация (convex combination) возникает как дальнейшее ограничение аффинной комбинации: не только сумма коэффициентов линейной комбинации должна равняться единице, но каждый коэффициент, кроме того, должен быть неотрицательным. Таким образом, линейная комбинация из равенства (4.3) является выпуклой, если
4.2. Обзор векторов
ai + a2+…+am-l (4.5)и а{> 0 для i - \,…,т.
Следовательно, все а{ должны находиться между 0 и 1. (Почему?)
Таким образом, 0,3а + 0,7b является выпуклой комбинацией векторов а и Ь, в то время как 1,8а - 0,8b - нет. Совокупность коэффициентов ava2,…,am иногда называют разбиением единицы (partition of unity), подразумевая под этим, что единичное количество «материала» разбивается на части. Выпуклые комбинации зачастую возникают в приложениях, где кто-то составляет единичное количество некоторой «смеси» и может комбинировать только положительные количества различных ингредиентов. Такие комбинации появляются в самых неожиданных контекстах. Например, мы увидим в главе 11, что сплайн-кривые фактически являются выпуклыми комбинациями некоторых векторов, а в наших исследованиях цвета (в главе 12) узнаем, что любой цвет единичной яркости можно представить в виде выпуклой комбинации трех простых цветов!
Нам представляется полезным понятие «множество всех выпуклых комбинаций» некоторого набора векторов. Для двух векторов v4 и v2 множество всех выпуклых комбинаций представляет собой множество всех векторов вида
v = (1 - a)v, + av2, (4.6)где параметр а может изменяться от 0 до 1. (Почему?) Что это за множество? Преобразуя равенство (4.6), получим:
v-yl+a(v3-yl). (4.7)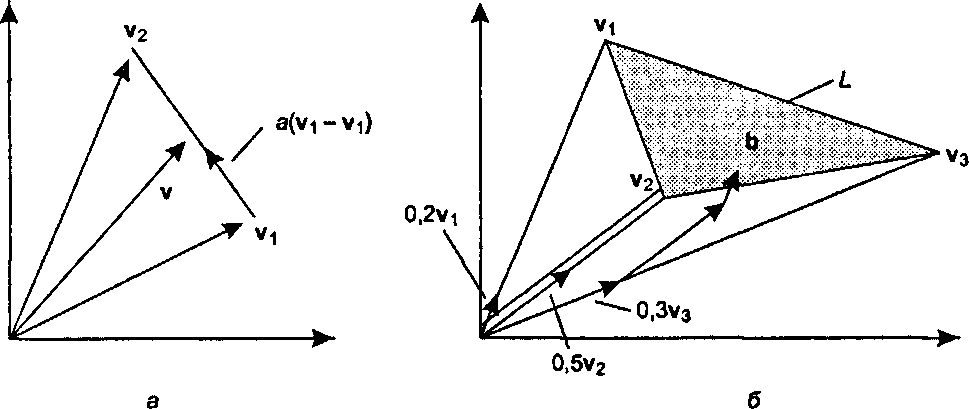
Рис. 4.8. Множество векторов, представимых выпуклыми комбинациями На рис. 4.8, а показан вектор v, равный сумме v, и некоторой части от \2- v,, причем конец вектора v расположен на прямой, соединяющей v, и у2. Так как а изменяется от 0 до 1, конец v может занимать положения, совпадающие со всеми точками отрезка прямой, соединяющего концы v, и у2, и только эти положения.
