Л в) =---, (3.21)
1±есоз(9) '
где е - эксцентриситет сечения. При в = 1 кривая является параболой, при 0 < е < 1 - эллипсом, а при е> 1 - гиперболой.
Дополнительные инструменты для рисования
Логарифмическая спираль
Логарифмическая спираль (logarithmic spiral) (она же изогональная спираль) /(0) = Ке"0, график которой приведен на рис. 3.63, а, также представляет определенный интерес [Coxeter, 51]. Эта кривая пересекает все радиальные линии под постоянным углом а, причем а = ctg(oc). Логарифмическая спираль - это единственная из спиралей, которая сохраняет свою форму при любом изменении масштаба: увеличьте фотографию логарифмической спирали в любое число раз, и увеличенная спираль в точности совпадет (после поворота) с исходной кривой. Подобным же образом, если вы будете вращать изображение изогональной спирали, вам будет казаться, что она становится больше или меньше [Steinhaus, 191 J1. Такая неизменяемость формы используется некоторыми животными, например моллюском, известным под именем наутилус помпилиус («chambered nautilus*), или просто кораблик (см. рис. 3.63, б). По мере роста моллюска его раковина также растет по логарифмической спирали, обеспечивая тем самым домик постоянной формы [Gardner, 76].
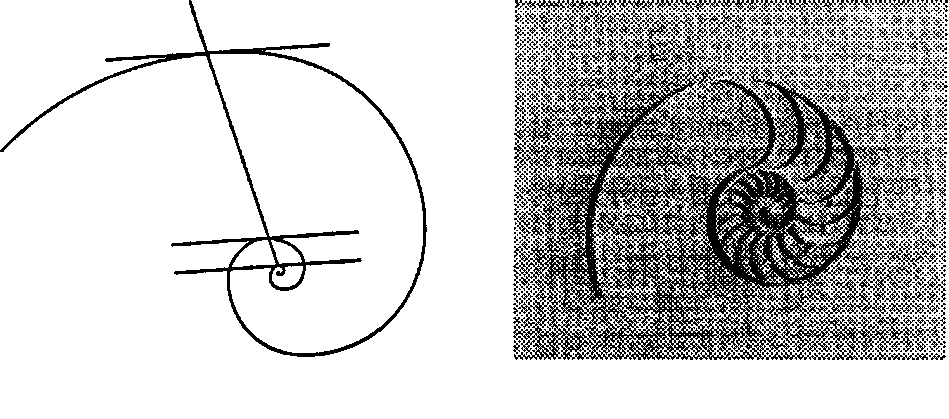
а б Рис. 3.63. Логарифмическая спираль (а); моллюск наутилус (б)
В упражнениях и тематических заданиях рассматриваются некоторые другие семейства кривых, а исчерпывающий список и описание интересных кривых дано в работах [Yates, 217, Seggern, 182, Shikin, 185].
3.8.5. Трехмерные кривые Кривые, которые изгибаются в трехмерном пространстве, также могут быть представлены параметрически и будут подробно рассмотрены в последующих главах. Для построения параметрической формы трехмерной кривой придумаем три функции х(.), у(.) и z(.) и предположим, что эта кривая находится «в точке» P(t) - (x(t),y(t), z(t)) в момент времени t. Рассмотрим несколько примеров.
Винтовая линия (геликоид)
Винтовая линия (circular helix) задается параметрически следующим образом: x(t) - cos(t).