y(t) = sin(0, (3.22) z(t) - bt,

где b - некоторая константа. Эта кривая показана на рис. 3.64 в виде стереопары. (Инструкции по просмотру стереопар смотрите в предисловии.) Если такое представление покажется вам слишком громоздким, сосредоточьтесь на одном из рисунков.

1 Эта кривая впервые была описана Декартом (Descartes) в 1638 году. А Якобу Берпулли (Jacob Bernoulli) эта спираль нравилась настолько, что она была выгравирована на его надгробном памятнике в Базеле, Швейцария, вместе с надписью «Eadem mutata resurgo», что означает «Измененная, я остаюсь прежней».

анализ образцов пищевых продуктов.

3,8. Применение параметрического задания кривой

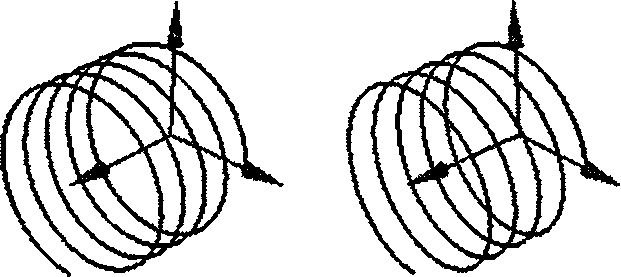
Рис. 3.64. Винтовая линия, изображенная в виде стереопары

Существует много разновидностей винтовой линии, например эллиптическая винтовая линия (elliptical helix), заданная формулой P(t) - (Wcos(t), #sin(r), bt), коническая винтовая линия (conical helix), описываемая равенством P(t) = (£cos(r), tsin(r), bt). (Нарисуйте их схематически.) Вообще говоря, любую двумерную кривую вида (x(t), y(t)) можно превратить в винтовую линию путем добавления z(t) = bt или какой-нибудь другой зависимости для z(t).

Тороидальная спираль

Тороидальная спираль (toroidal spiral), заданная формулой x(t) - (asin(cr) + è)cos(r),

y(t) - (asin(cr) + b) sin(c), (3.23) z(t) - acos(cc),

может быть образована нитью, намотанной на тор (трехмерное тело в форме баранки). На рис. 3.65 представлен случай с - 10, то есть нить делает 10 оборотов вокруг тора. В главе 6 мы будем рассматривать трубы, образованные такой спиралью.

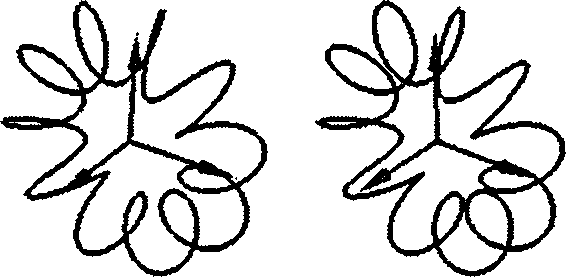
Рис. 3.65. Тороидальная спираль, изображенная в виде стереопары

Практические упражнения

3.8.6. Рисование суперэллипсов Напишите подпрограмму drawSuperE^ 1т рэе(…), которая рисует суперэллипс. Эта подпрограмма имеет следующие параметры"opengl1_196.html">⇐ Предыдущая| |Следующая ⇒