2. Выбираем в качестве начальной точки для рисования р0 одну из точек Г0, Тр Т2 случайным образом.
1 В математической литературе прошлых лет эта фамилия переводится как Серпиньский. - Примеч. пер.
А_
Моя первая попытка
-1^.Рис. 2.5. Простое созвездие точек
Начальная стадия: рисование фигур
Теперь будем выполнять итерационный процесс до тех пор, пока поле рисунка не будет заполнено в достаточной степени.
1. Выберем случайным образом одну из точек Т0, Т1У Т2и обозначим ее Т.
2. Вычислим следующую точку рк как середину1 отрезка между точкой Г и найденной ранее точкой рку Это означает, что рк является серединой отрезка, соединяющего точки рк1 и Т.
3. Рисуем точку рк с помощью функции о"га>/0от.().
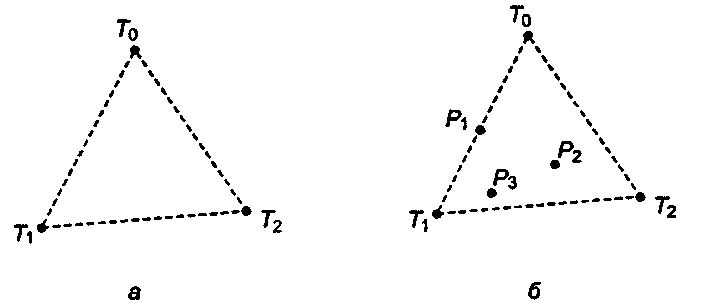
Рис. 2.7. Построение ковра Серпинского Рисунок 2.7, б отображает несколько итераций описанной процедуры. Пусть начальной точкой будет Т0, а следующей выбрана точка Г,. В этом случае точка pt ляжет посередине между рх и Г,. Пусть далее выбрана точка Т2, так чтор2 ляжет посередине между р, и Т2 Пусть далее опять выбрана точка Г,, так что р3 будет вычислена по приведенной схеме и т. д. Данный процесс продолжает создавать и рисовать точки (теоретически бесконечно), и на экране быстро появляется орнамент ковра Серпинского.
Представляется удобным определить простой класс GlintPoint, описывающий точку с целыми координатами2"opengl1_103.html">⇐ Предыдущая| |Следующая ⇒