int random (int m) {
return randOftn;
)1 Для того чтобы найти среднюю точку между двумя точками, например (3,12) и (5,37), нужно просто вычислить среднее арифметическое каждой пары координатой у, сложив их и разделив на два. Таким образом, средняя точка между (3,12) и (5,37) -= ((3+5)/2, (12+37)/2) - (4,24).
2 Если используется С, а не С++, то здесь подойдет простая структура typedef struct Glint х.у;} GlintPoint:.
3 Напомним, что стандартная функция rand () возвращает псевдослучайную величину в диапазоне от 0 до 32767. Функция пересчета по модулю уменьшает этот диапазон до уровня от 0 до 2.
городская олимпиада по геометрии.
2.2. Рисование основных графических примитивов В листинге 2.6 приведены остальные детали алгоритма, который генерирует 1000 точек ковра Сер-пинского.
Листинг 2.6. Генерирование ковра Серпинского
void Sierpinski(void)GLintPoint Т[3гаі0.10}.(300.300.(200.300)}:
int index - random(3): // 0, 1 or 2 equally likely // 0, 1 или 2 равновероятны
GLintPoint point - T[index]: // initial point // начальная точка
drawDot(point.x. point.у): // draw initial point // рисуен начальную точку
fordnt і - 0: і < 1000: і++) // draw 1000 dots // рисуєм 1000 точек
{
index random(3):point.x - (point.x + T[index].x) / 2; point.у - (point.y + T[index].y) / 2: d rawDot(poi nt.x.poi nt.у):
}
glFlushO:
}Пример 2.2.3. Простейшие «точечные рисунки» («Dot Plots»)
Предположим, что вы хотите изучить поведение некоторой математической функции f(x) от переменной х. Например, как изменяется
f(x) - e~xcos(2rc х)
при изменении аргумента х от 0 до 4? Многое может прояснить быстрый график, построенный в осях f{x) и х, подобный приведенному на рис. 2.8.
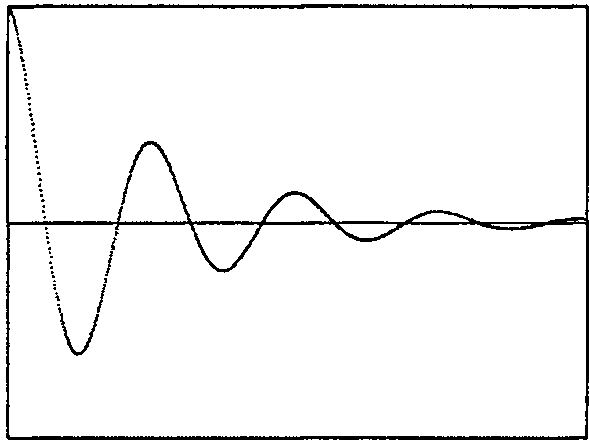
Рис. 2.8. «Точечный график» зависимости функции f (x) = e_xcos(2nx) от аргумента х
