Переход к аналитическим методам анализа и синтеза силлогизмов предельно прост и основан на скалярных диаграммах. По скалярным диаграммам заполняются таблицы истинности, а по ним классически синтезируются Булевы функции. На основании аналитического представления силлогистических функторов и скалярных диаграмм автором были разработаны простые и прозрачные, «как геометрия», алгоритмы анализа и синтеза силлогизмов[2,3]. В них применена жёсткая, но примитивная математика, понятная школьнику[4,5].

Классическая силлогистика не имеет никакого отношения к здравому смыслу и математике, обременена множеством ненужных определений, законов, правил и т.п. и не воспринимается студентами. Кроме того, классическая силлогистика далеко не всегда корректна[4]. Именно поэтому автору пришлось разработать силлогистику здравого смысла. Новые методы доказательства законов в логике суждений, алгоритмы анализа и синтеза силлогизмов вместе с новыми методами решения логических уравнений, нахождением обратных функций, анализом и синтезом соритов составили Русскую логику, названную так в честь великих русских предшественников, заложивших её основание и в честь того, что «техническое задание» Лейбница было выполнено в России русским инженером. Таким образом, Россия вновь оказалась в лидерах мировой науки, в лидерах решения стратегических проблем ИИ.

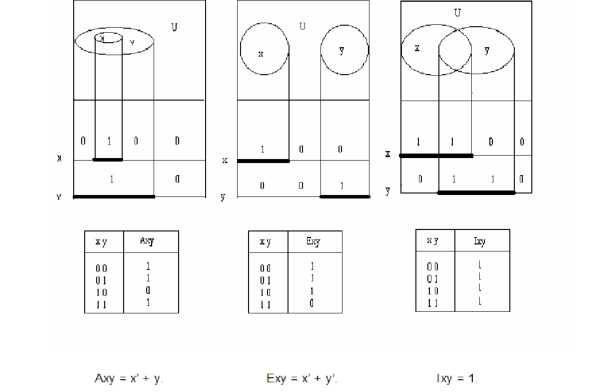
Рис. 3.1. Переход от диаграмм Венна к диаграммам Лобанова и синтез силлогистических функторов Аху, Еху, 1ху.

Для того, чтобы донести Русскую логику до отечественных студентов, я по совместительству, т.е. в свободное от основной работы время, интенсивно преподавал её в школах, лицеях, техникумах, колледжах и академии приборостроения. Результаты вполне успешные: школьники и студенты легко осваивают примитивную математику. Были случаи, когда в числе моих студентов оказывались семиклассники. Однако массового внедрения логики в обучение не произошло. Скоро студенты и школьники будут смеяться над преподавателями, излагающими невежественную классическую логику: Шете! доступен всем.

Как видим, общеутвердительный функтор описывается по Порецкому, по Кэрроллу и по Лобанову формулой: Аху = х’ + у. Импликация имеет тот же математический вид: х-- у = х’ + у. Да и общеразговорные значения этих операторов одинаковы. Мы говорим: «Все люди талантливы». Этот же смысл сохранится в суждении: «Если ты человек, то ты талантлив». Следовательно, разделение на логику суждений и логику предикатов бессмысленно.

При синтезе заключений зачастую имеют место несколько вариантов решений. Рассмотрим следующий силлогизм.

Задача.

Пусть М = АшхАшу и пи = 5, пМ = 2, пХ = 3, пУ = 4. Найти заключение.

Решение.

Из скалярных диаграмм получим такие результаты. п(Ашу) = С(3,2) = 3, п(Аху) = С(2,1) = 2, п(1ху) = 1.

⇐Применение новых технологий в информатике-стр.29 | Применение новых технологий в информатике | Применение новых технологий в информатике-стр.31⇒