if(objExists(“myCurve”)==1) { delete “myCurve"; } curve -p 0 0 0 -n "myCurve”; int $i;
for($i=0; $i< 100; $i=$i+1)
{
float $t=$i/10.0; float $x=$t; float $y=sin($t);
curve -p ($x) ($y) 0 -a “myCurve”;
}
Замечание про Undo. Как вы уже наверное заметили, MAYAисправно отменяет все действия, производимые нашим скриптом, то есть сохраняет в очереди Undo наши процедурные телодвижения. Мой опыт показывает, что если длина очереди Undo задана бесконечной в преференциях MAYA, то в результате многоразового выполнения довольно длинных циклов на MEL, связанных с созданием и изменением объектов, оперативная память может слегка закончиться. Поэтому я советую перед экспериментами с процедурным моделированием и программированием многошаговых циклов установить длину очереди Undo в небольшое значение, например, десять.
Кроме того, существует довольно полезная команда flushUndo, позволяющая одним махом очистить всю очередь Undo. Ее можно использовать не только в конце скриптов, но и после многочасовой смены по моделированию чего-нибудь.
Теперь вы можете дать волю своим фантазиям и попытаться построить графики всех известных вам функций (если таковые имеются). Те, кто с детства мечтал увидеть функцию noise, могут быстро изменить всего одну строку и получить долгожданный график.
if(objExists("myCurve”)==1) { delete “myCurve”; } curve -p 0 0 0 -n "myCurve”; int $i;
for($i=0; $i<100; $i=$i+1)
£
float $t=$i/10.0;
float Sx=$t;
float $y=noise($t);
curve -p ($x) ($y) 0 -a "myCurve”;
}
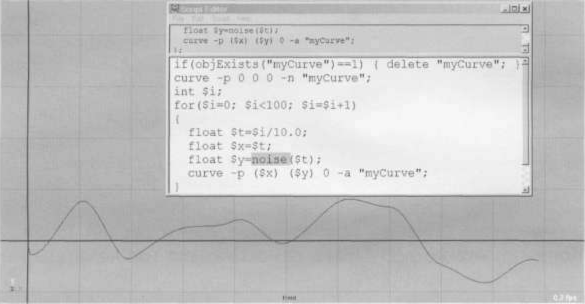
Как видите noise напоминает «сильно помятый» синус.
Я также предложу выйти из плоскости в пространство и построить спираль по формулам, хорошо известным любому второкласснику. Для этого понадобится еще одна переменная $z.
if(objExists(“myCurve”)==1) { delete “myCurve”; } curve -p 0 0 0 -n “myCurve”; int $i;
for($i=0; $i<100; $i=$i+1) t
float $t=$i/10.0; float $x=$t; float $y=sin($t); float $z=cos($t);
curve -p ($x) ($y) ($z) -a “myCurve”;
}
Для того, чтобы спираль была подлиннее, надо увеличить число точек до пятисот и уменьшить ее скорость раскручивания по оси X.
if(objExists(“myCurve”)==1) { delete “myCurve”; } curve -p 0 0 0 -n “myCurve”; int $i;
for($i=0; $i<500; $i=$i+1)
I
float $t=$i/10.0; float $x=$t/5.0; float $y=sin($t); float $z=cos($t);
curve -p ($x) ($y) ($z) -a “myCurve”;
}
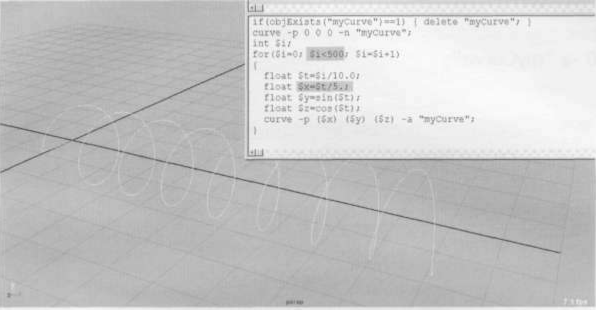
Одна деталь наверняка смущает причирчивые умы - первая точка, которая ставится в начало координат. Конечно, можно добавить в самом начале три команды вычисления $х, $у, $z при $t=0 и ставить первую точку командой
curve -р ($х) ($у) ($z) -n “myCurve”; Однако ленивые умы просто подсмотрят команду удаления первой точки в Script Editor и вставят ее в конец скрипта.
curve -р ($х) ($у) ($z) -a “myCurve”;
]
delete “myCurve.cv[0]”; Теперь вы в очередной раз можете реализовать свои тайные наклонности и поиздеваться над формой спирали. Помните, что множители перед sin и cos задают радиус (амплитуду) спирали, а множители перед $t определяют частоту колебаний.
if(objExists(“myCurve”)==1) { delete “myCurve”;} curve -p 0 0 0 -n “myCurve”; int $i;
