}
Таким образом, с минимальными исправлениями универсальный скрипт для работы с выделенными объектами превращается в подобие noise deformer, и он модифицирует форму объекта случайным образом. Этот скрипт будет работать с выделенными вершинами не только на сплайновых поверхностях, но и на кривых, полигональных сетках и даже на решетках типа Lattice, причем вы можете одновременно выбирать компоненты разных объектов и запускать скрипт на выполнение.
Затащите его на полку и не забудьте сделать: File=>Save Preferences.
Примечание. Флаг -fl никак не влияет на вид списка в случае, когда выбраны объекты, а не компоненты, так что можете использовать его всегда, для универсальности.
Если вы измените для сферы количество sections/spans до 50, то есть радикально увеличите количество вершин, а затем выберете все вершины и запустите деформер-скрипт, его выполнение займет ощутимое время.
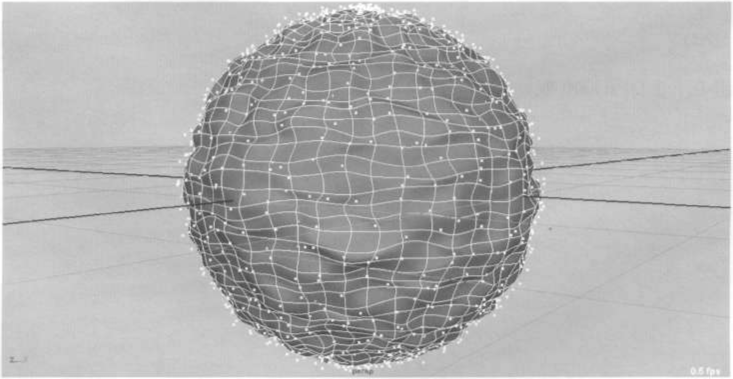
Граница применимости MEL
Вышеприведенный пример очень четко обозначает границу применимости MEL. Так как команды языка выполняются ядром MAYA, а не самой операционной системой (технически говоря, MEL - интерпретируемый язык), в случае интенсивных или сложных вычислений его производительность невысока. Он предназначен для автоматизации, а не для сложных расчетов. И в тот момент, когда его производительности вам начнет не хватать, вам придется задуматься об освоении MAYA API и работе с MAYA SDK.
Кроме того, если вы захотите написать полноценный деформер, так чтобы деформация поверхности имела Construction History, то есть ноду, в которой можно задавать величину деформации, вам никуда уже не деться от C++ и от MAYAAPI. С помощью скриптов нельзя задавать операции, имеющие Construction History, можно лишь выполнить последовательность действий, нажать Undo, изменить значения переменных и выполнить скрипт снова. Это принципиальный момент.
Процедурное моделирование Разберем далее, как можно использовать MEL-команды для моделирования, то есть для построения геометрии с помощью формул. А заодно разберем еще одну конструкцию цикла и применение условных переходов.
Начнем с наивного использования метода пристального взгляда.
В новой сцене нарисуйте кривую любым способом.
Загляните в Script Editor и найдите там последнюю команду, напечатанную в верхней части окна. Она выглядит примерно так:
curve -d 3 -р 9.116545 0 11.562727 -р 1.740198 0 7.561535 -р -2.160891 0 2.562245 -р 0.675565 0 -1.455057 -р 7.176817 0 -0.665676 -к 0 -к 0 -к 0 -к 1 -к 2 -к 2 -к 2 ; Суда по всему, флаг -d задает степень кривой, а флаги -р определяют координаты контрольных вершин кривой. Остальные флаги нас пока не интересуют.
Наберите и выполните команду
curve -р 0 0 0; После этого в начале координат (в точке 0 0 0) возникнет кривая, состоящая из одной (!) точки. Вы можете убедиться в этом, выбрав ее и исследовав в Attribute Editor.
Очевидно, что если выполнить команду:
curve -р 0 0 0 -р 0 1 0 -р 1 1 0 -р 1 0 0; то возникнет сегмент кривой третьего порядка (значение флага -d по умолчанию равно трем).
Однако идея состоит в том, чтобы поставив одну точку, добавлять к ней новые вершины в цикле, добиваясь «выращивания» кривой по некоторой формуле.
