Теперь вернемся к тарелке на столе.
В новой сцене создайте полигональный цилиндр.
Сожмите его по вертикали до состояния «тарелки» и приподнимите немного (trans-lateY=0.5).

Теперь поверните цилиндр на 30 градусов вокруг оси Z. Его край коснется «земли».
Тут пытливые умы сообразят, что радиус цилиндра равен единице и что угол в тридцать градусов был взят не с потолка, а в результате сакральных вычислений, заключающихся в следующем: если радиус цилиндра (равный единице) - это гипотенуза прямоугольного треугольника, а положение его центра по вертикали - катет (равный 0,5), то угол напротив этого катета должен быть равен 30 градусов, ибо синус от 30 градусов равен в точности 0,5.
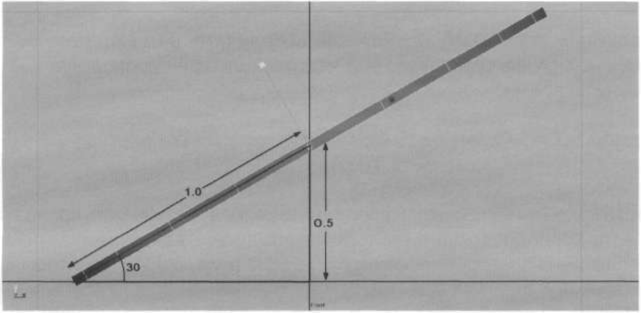
Давайте напишем expression, который будет вычислять угол поворота тарелки в зависимости от высоты, так, чтобы она всегда касалась «земли».
Откройте Expression Editor и создайте новый expression:
pCylinderl .rz=asind(pCylinder1 .ty); Загадочная функция asind - это арксинус (функция, обратная синусу), возвращающий значение в градусах (буква d на конце - это от degree).
Теперь, если вы будете таскать тарелку вверх-вниз, она всегда будет касаться одним краем земли.
Теперь попробуем закрутить тарелку.
Оказывается циклические выражения, упомянутые выше, применимы не только к перемещениям, но и к любым другим атрибутам. Чтобы заставить, например, циклически поворачиваться нашу тарелку, можно просто написать формулу:
//pCylinderl .rotateZ=asind(pCylinder1 .translateY);
pCylinderl ,rotateX=30*sin(time*5);
pCylinderl. rotateZ=30‘cos(time*5); Две косые черты - знак комментария, и все, что следует за ним до конца строки, при выполнении expression игнорируется.
Сейчас тарелка весело вращается вокруг вертикальной оси, наклоняясь на 30 градусов. Для угла наклона у нас уже есть формула, осталось подставить ее вместо числа 30. Используем для этого переменную:
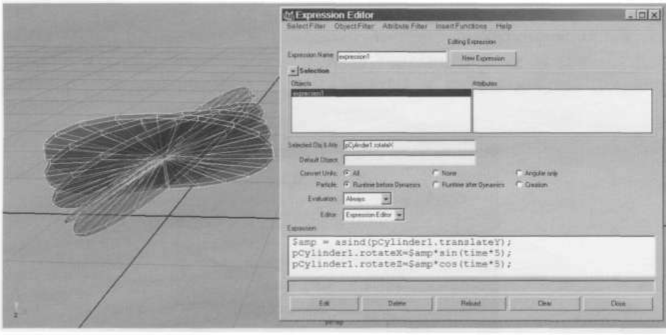
Samp = asind(pCylinder1 .translateY);
pCylinderl. rotateX=$amp‘sin(time*5);
pCylinderl. rotateZ=$amp*cos(time*5); Теперь тарелка вращается под нужным углом в зависимости от высоты ее центра (не задирайте пока тарелку выше единицы).
Число 5 в формулах задает частоту колебаний. Эта частота должна возрастать по мере того, как тарелка опускается на «землю», а у самой земли тарелка должна неистово дребезжать.
Зададим формулу для вычисления частоты колебаний в зависимости от высоты центра тарелки, то есть от значения атрибута translateY.
Sspeed = 5.0/(pCylinder1 .translateY+0.01);
$amp = asind(pCylinder1. translateY);
pCylinderl .rotateX=$amp*sin(time*$speed );
pCylinderl ,rotateZ=$amp*cos(time*$speed ); Теперь, если высота центра близка к единице, то тарелка вращается с прежней частотой, приблизительно равной 5, а если опускать тарелку, то ее вращение стремительно ускоряется. Это можно увидеть, и не запуская анимацию, а лишь «таская» тарелку вверх или вниз. Добавление числа 0.01 необходимо для того, чтобы избежать деления на ноль, когда центр тарелки вдруг опустится на «землю».
В принципе expression готов. Для того, чтобы анимировать «устаканивание» тарелки, вам достаточно поставить ключи на атрибут translateY. Это даст вам возможность уложить ее на землю именно так, как, по-вашему, должны вести себя фотореалистические тарелки. Она может подниматься и опускаться столько раз, сколько вам нужно. Если вы до того прониклись революционными идеями процедурной анимации, что не можете более ставить ключи, можете дописать в expression дополнительную строчку для анимации translateY, например
