Функция clamp(x, minVal, maxVal) не имеет наклона при х, меньшем rninVal, и х, большем maxVal, и имеет наклон при х, большем mi nVa 1 и меньшем maxVal. Она функционально эквивалентна выражению min(rnax(x, minVal), maxVal).
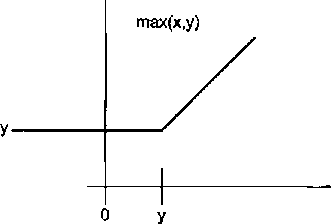
Рис. 5.9. Функция max
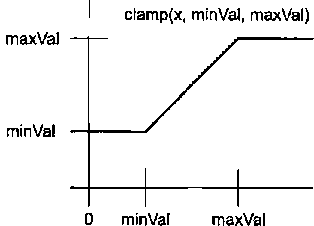
Рис. 5.10. Функция clamp
Функция step может использоваться для создания бесконечной прямой со сменой значения в конкретной точке (рис. 5.11). Использование этой функции рас-ематривается в главе 6 на примере создания простого процедурного шейдера.
Функция smoothstep (рис. 5.12) может быть полезна в случае, если в определенной точке нужен плавный переход от одного значения к другому. Например, если t- float, это эквивалентно float t:
t = clamp (Cx - edgeO) / (edgel - edgeO). 0,0. 1.0): return t * t * (3.0 - 2.0 * t): Случаи использования других параметров - векторов vec2, vec3 и vec4 - отличаются от приведенного примера только типом данных t.
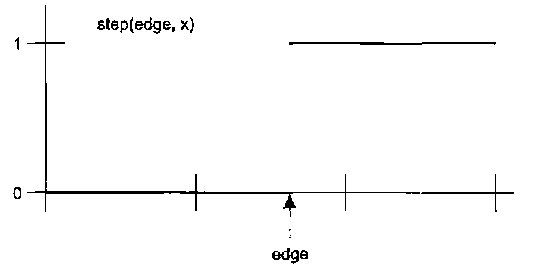
Рис. 5.11. Функция step
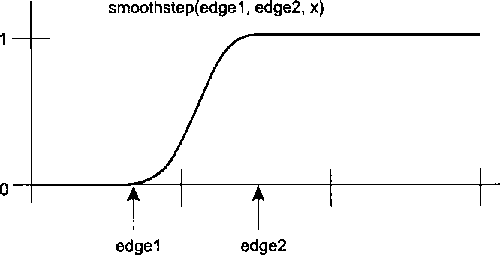
Рис. 5.12. Функция smoothstep
5.4. Геометрические функции
Геометрические функции, исключая ftrgnsform, можно использовать и из вершинного, и из фрагментного шейдера. Эти функции работают с параметрами-векторами как с настоящими векторами, а не поэлементно (табл. 5.4).
Таблица 5.4. Геометрические функции
|
Синтаксис |
Описание |
|
float length (float х) float length (vec2 x) float length (vec3 x) float length (vec4 к) |
Возвращает длину вектора х, то есть sqrt(jr[0] ■ *•[£)] + *[1] ■ х[1] + …) |
|
float distance (float pO. float pi) float distance (vec2 pO. vec2 pi) float distance (vec3 pO, vec3 pi) float distance (vec4 pO, vec4 pi) |
Возвращает расстояние между рО и pi, то есть length (pO- pi) |
|
float dot (float x. float у) float dot (vec2 x. vec2 y) float dot (vec3 x. vec3 y) float dot (vec4 x. vec4 y) |
Возвращает скалярное произведение хи у, то есть result = *[0] - /[0] + х[1] ■ у\ 1] +… |
|
vec3 cross (vec3 x. vee3 y) |
Возвращает векторное произведение хи у то есть result[0] = х[1] ■ у [2]- у [1] ■ х[2] resultfl] = л-[2] • у[0] - у[2] - лг[0] result[2] = *[0] ■ /[1] - /[0] • *[1] |
|
float normalize (float x) vec2 normalize (vec2 x) vec3 normalize (vec3 x) vec4 normalize (vec4 x) |
Возвращает вектор с тем же направлением, что х, но длиной 1 |
|
Синтаксис |
Описание |
|
vec4 ftransformO |
Только для вершинных шейдеров. Эта функция гарантирует, что координаты вершин будут преобразованы таким же способом, что и обычными операциями OpenGL. Предполагаемое применение этой функции - вычисление значений для gl^Position |
|
float faceforward (float N. |
Если скалярное произведение (Nref, I) < 0,0, |
|
float I, float Nref) vec2 faceforward (vec2 N, ■vec2 I, vecZ Nref) vec3 faceforward Cvec3 N. vec3 1. vec3 Nref) vec4 faceforward Cvec4 N. vec4 1. vec4 Nref) |
вернуть N; в противном случае вернуть -N |
|
float reflect (float I. |
Для инцидентного вектора Iи ориентации поверх |
|
float N) |
ности N возвращает направление отражения: |
|
vec2 reflect (vec2 I. |
result = I- 2,0 ■ dot(/V, I) - N |
|
vec2 N) vec3 reflect (vec3 1, vec3 N) vec4 reflect [vec4 I. vec4 N) |
/Удолжно быть нормализовано |
Версия функции di stance с параметрами fl oat, возможно, не очень полезна (это то же самое, что абсолютное значение разницы), но при этом вычисляется расстояние Эвклида между двумя точками. Подобным образом Л oat-версия функции normal i ze всегда будет возвращать 1, a f 1 oat-версия функции 1 ength всегда будет возвращать абсолютное значение входного аргумента. Скалярные формы этих функций полезны тем, что типы данных аргументов могут быть изменены без изменения кода, который будет вызывать встроенную функцию.
