Так как комплексные числа состоят из двух частей, множество комплексных чисел является двухмерным. Их можно обозначить на плоскости, где горизонтальная ось представляет вещественную часть числа, а вертикальная - мнимую (рис. 15.6).
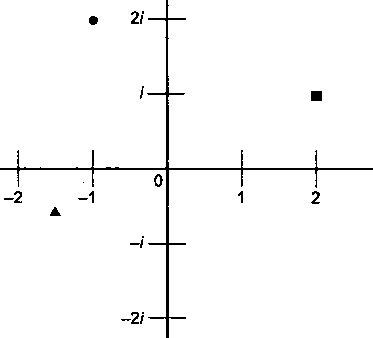
Рис. 15.6. Пример обозначения комплексных чисел на плоскости Для некоторых значений с функция уходит в бесконечность, для некоторых - нет. Все очень просто: значения с, уходящие в бесконечность, не являются частью множества Мандельброта. Используя компьютер (или графический ускоритель с поддержкой языка шейдеров OpenGL) для проверки тысяч точек на плоскости комплексных чисел и помечая серым цветом точки, уходящие в бесконечность, и черным цветом - все остальные точки, получим геометрическую фигуру сердцевидной формы (рис. 15.7).
Как же проверить, какие значения уходят в бесконечность? Мандельброт определил это. Он показал, что если модуль Z (расстояния от начала координат) больше 2, значение функции всегда бесконечно. Чтобы запрограммировать эту функцию, нужно остановить итерации, когда модуль Z превысит значение 2. И даже проще, так как мы все время работаем с Z2, сравнивать это значение с 4.
Значения внутри черной фигуры на рис. 15.7 не уходят в бесконечность за : некоторое разумное количество итераций. Чтобы не зацикливать графический акселератор, нужно определить максимальное количество итераций, после проведения которых предполагается, что точка принадлежит множеству Мандельброта. На основе этих двух критериев можно написать простой цикл, вычисляющий множество Мандельброта.

Рис. 15.7. Графическое представление множества Мандельброта Изображение будет более красочным, если закодировать количество итераций разными цветами. Значения, которые оказались вне множества после первой итерации, обозначаются одним цветом; значения, «выброшенные» на следующей итерации, обозначаются другим цветом и т. д. На рис. 15.7 вместо разных цветов использованы оттенки серого. Белые точки вдоль края были вычислены за 20 итераций.
Края множества Мандельброта бесконечно разнообразны при разном количестве итераций. Продолжая вычисления, можно выявить точки вне множества на сотых или даже тысячных итерациях.
Вот несколько соображений по поводу рисования множества Мандельброта.
□ Длина края бесконечна.
□ Все области внутри множества Мандельброта (обозначенные черным цветом) сообщаются.
□ Для каждой итерации существует только одна полоса, огибающая множество Мандельброта. Полосы полностью окружают изображение, не пересекаются и не прерываются. При увеличении края получается интересное изображение.
□ Существует бесконечное количество «мини-Мандельбротов» (частей, по форме похожих на искаженное или трансформированное изображение основного множества).
15.3.2. Вершинный шейдер
Вершинный шейдер для множества Мандельброта (листинг 15.6) почти такой же, как вершинный шейдер кирпичной стенки из раздела 6.2. Единственное отличие - текстурные координаты в диапазоне [0, 1] представляются и для s, и для t. Эти значения отображаются на диапазон [-2,5, 2,5], и результат сохраняется в varyingпеременной Position. Это дает фрагментному шейдеру возможность рисовать точки непосредственно в системе координат, центром которой является точка (0, 0). Если приложение рисует прямоугольник, размер которого совпадает с размером экрана и имеет текстурные координаты левого нижнего угла (0, 0) и правого верхнего угла (1, 1), в результате получится стандартное представление множества Мандельброта. С помощью шейдера Мандельброта на языке шейдеров OpenGL области можно «текстурировать» любым образом и даже накладывать простое освещение.
