12.1. Определение шума
Цель этого раздела - не описывать математически функции шума, а дать читателю достаточно информации для понимания шейдеров, использующих шум, и создания новых эффектов на основе этой технологии. Чтобы глубже разобраться в технологии шума, следует обратиться к литературе, ссылки на которую приведены в конце этой главы, особенно к книге [2], в которой обсуждается технология шума, в том числе и самая первая функция шума, созданная К. Перлином. В этой книге Дарвин Пичи (Darwyn Peachey) систематизирует функции шума. Наложение функций шума и различные их сочетания описаны Кеном Масгрейвом (Кеп Musgrave) в главе о построении изображений планет процедурно.
Перлин описывает шум как «приправы* для графики. Эти функции помогают добавлять изображению небольшие дефекты, но их влияние навнешний вид объекта не исчерпывается только этим. Идеальная модель должна выглядеть не идеально (иметь погрешности и дефекты) и поэтому более реалистично, так как на нее накладываются едва различимые эффекты шума.
Идеальная функция шума должна обладать несколькими важными качествами,
□ Это непрерывная функция, которая создает впечатление случайной.
□ Это воспроизводящаяся функция (будет выдавать всякий раз одно и то же значение при задании одного и того же входного параметра).
Q Функция имеет определенный диапазон выходных значений (обычно [-1, 1] или [0, 1]).
□ Значения функции не должны формировать какого-либо очевидного регулярного шаблона или периода.
□ Функция не зависит от масштабирования.
□ Это изотропная функция (при статистическом повторении она должна быть инвариантной).
□ Функция может быть определена для 1, 2, 3,4 или больше измерений.
Такое определение шума подразумевает создание неровного примитива, который затем можно использовать для наложения видимых случайных элементов на повторяющийся шаблон, а также для моделирования, рендеринга или анимации. Характеристики функции шума позволяют получить с ее помощью весьма интересные эффекты. Алгоритмы для создания функций шума подразумевают компромисс качества и скорости, и приведенные ранее критерии способствуют выбору такого компромисса.
Простую функцию шума (называемую Пичи значение шума) можно создать, присваивая псевдослучайное число из диапазона [-1,1] каждому целому числу на осих (рис. 12.1), а затем плавно интерполируя значения между этими точками (рис. 12,2). Функция является повторяемой, то есть для определенного значения входного параметра все время возвращается одно и тоже значение функции.
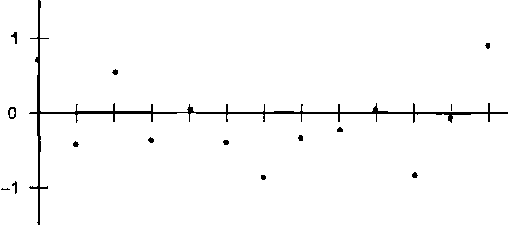
Рис. 12.1. Дискретная ID-функция шума
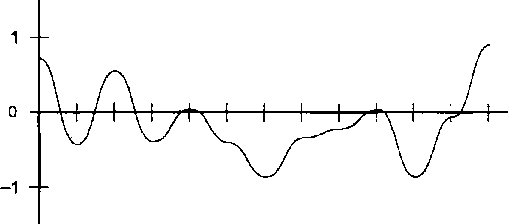
Рис. 12.2. Непрерывная ID-функция шума Выбор метода интерполяции между дискретными точками очень важен для этой разновидности функций шума. Линейная интерполяция недостаточно хороша, так как в результате наложения такого шума на изображении появляются де■фекты. Для получения плавных переходов обычно используется метод кубич ведой интерполяции.
