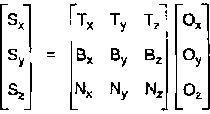
Рис. 11,3. Преобразование из пространства координат объекта в локальное пространство координат поверхности
11.4.1. Подготовка приложения
Чтобы шейдер бугристой поверхности работал правильно, приложение должно задать координаты вершины, нормаль поверхности и тангенциальный вектор в плоскости поверхности. Тангенциальный вектор передается как произвольный вершинный атрибут, а индекс атрибута должен быть связан с переменной вершинного шейдера tangent с помощью вызова функции gl Bi ndAtt ri bLocati onARB. Приложение также должно задать значения для uniform-переменных Li ghtPosi ti on, SLirfaceColor, BumpDensity, BimpSize и SpecularFactor.
Необходимо позаботиться о том, чтобы тангенциальные векторы были согласованы; в противном случае преобразования в локальные пространства также будут несогласованными, что сделает результаты вычисления освещения непредсказуемыми. Согласованные тацгенциал ьны е векторы могут быть вычислены алгоритмически для поверхностей, определенных математическими формулами. Согласованные тангенциальные векторы для сложных объектов можно вычислить с помощью соседних вершин, согласованно упорядочивая их с помощью текстурных координат объекта.
Проблема, связанная с несогласованно определенными нормалями, иллюстрируется рис. 11.4. На диаграмме показаны два треугольника: один с согласованными тангенсами, второй - с несогласованными. Серые стрелки указывают направление тангенциального вектора и вектора бинормали (нормаль поверхности направлена прямо вверх перпендикулярно странице). Белые стрелки показывают направление навстречу источнику освещения (в данном случае это направленный источник освещения).
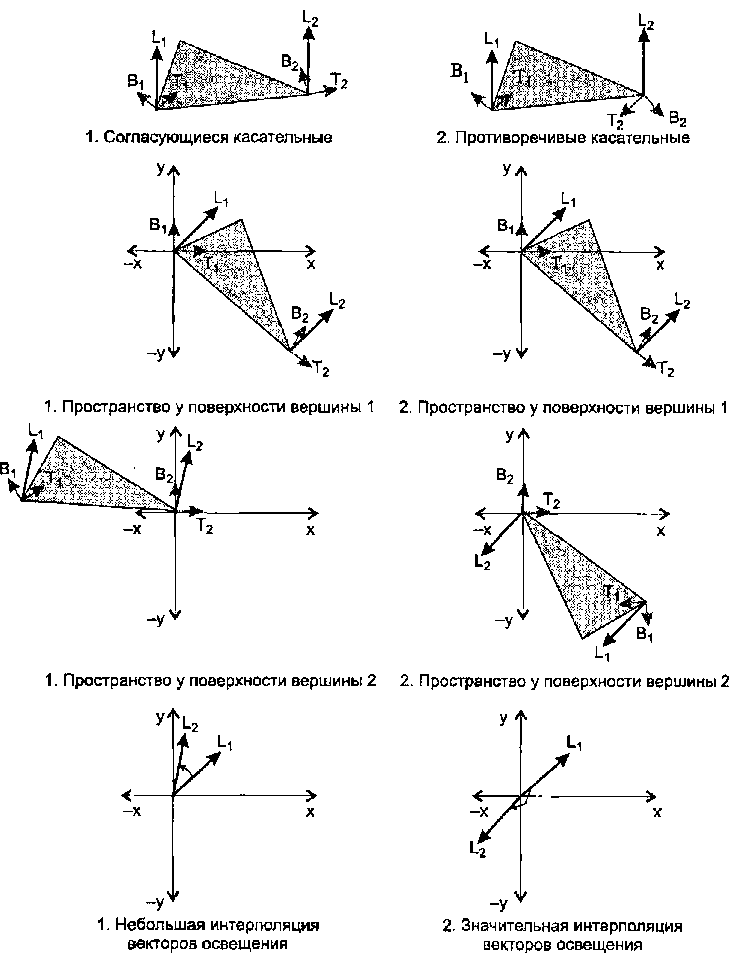
Рис. 11.4. Несогласованные тангенсы могут вызвать серьезные ошибки при вычислении освещения В обоих случаях при преобразовании вершины 1 в локальное пространство координат поверхности получается один и тот же результат. Но при преобразовании вершины 2 наблюдается большое отличие, так как тангенциальные векторы этих двух вершин очень разные. Если бы они были определены согласованно, этого бы Fie случилось, разве что поверхность стала бы очень изогнутой. И если это действительно так, можно разбить поверхность объекта на ячейки, чтобы предотвратить возможные проблемы.
В первом случае вектор направления освещения будет ровно интерполирован от первой до второй вершины, и все интерполированные векторы будут приблизительно одной длины. Если нормализовать этот вектор освещения в каждой вершине, его длина будет очень близка к единичной.
Но во втором случае векторы после интерполяции будут иметь разную длину, некоторые из них почти нулевые. Это может привести к дефектам изображения.
OpenGL не определяет конкретный вершинный атрибут для тангенциального вектора. Следует использовать произвольный атрибут вершины для передачи этого значения, так же, как это сделано в примере, приведенном в разделе 10.5.1. Един-стненное различие в том, что не приложение будет передавать бинормаль, а вершинный шейдер сам будет вычислять ее.
11.4.2. Вершинный шейдер
Вершинный шейдер для метода бугристой поверхности приведен в листинге 11.7. Этот шейдер должен вычислять направления освещения и обзора в локальном пространстве координат поверхности. Входные данные для шейдера - координаты вершины, нормаль поверхности, тангенциальный вектор. Шейдер вычисляет бинормаль и преобразует координаты с помощью созданной матрицы преобразования. Текстурные координаты тоже передаются в вершинный шейдер, так как текстура используется для задания координат процедурных бугорков.
