float inorout: // Счетчик для вычисления шаблона звезды
Сперва преобразуем точку на поверхности, которую нужно закрасить, в точку на сфере радиусом 1,0. Сделать это можно с помощью функции normal ize:
p.xyz = normalize(ECposition.xyz - ECbal1 Center.xyz): p.w =1.0: Координата w в вычислениях не используется, поэтому применяется оператор выбора компонентов .xyz для выбора первых трех компонентов ECposition и ECball-Center. Этот нормализованный вектор затем сохраняется в первых трех компонентах р. После этих вычислений р представляет точку на сфере с радиусом 1, так что все три компонента р будут находиться в диапазоне [-1, 1 ]. Координата w здесь не нужна, но для последующих вычислений она инициализируется в 1,0.
Затем определяется положение точек звезды по отношению к полупространствам. Счетчик i norout будет инициализирован в значение -3. Он будет увеличиваться все время, если точка на поверхности является внутренней по отношению к полупространству. Так как определено пять полупространств, окончательное значение счетчика будет находиться в диапазоне [-3, 2]. Значения 1 или 2 будут означать, что фрагмент находится внутри звезды. При значениях 0 или меньше фрагмент находится вне звезды:
inorout = InOrOutlnlt: // инициализация 1 norout в -3
Мы могли бы определить полупространства как массив из пяти значений vec4, затем выполнить вычисления, а результаты сохранить в массиве из пяти значений f 1 oat. Но здесь можно получить некоторое преимущество в скорости, используя параллельность графического аппаратного обеспечения. Рассмотрим эту процедуру. Сначала с помощью встроенной функции dot вычисляется расстояние между р и первыми четырьмя полупространствами:
distance[0] = dotCp, HalfSpaceO): distanced] = dot (p. Hal fSpacel >: distanced] = dotfp. HalfSpace-2): distance[3] = dotCp. HalfSpace3): Результаты этих вычислений показаны на рис. 11,1, а-г. Точки на поверхности, которые определены как внутренние, показаны серым цветом, а определенные как внешние - черным цветом.
Наверное, читатель удивлен, почему счетчик был определен как fl oat, а не как
i nt. Но счетчик является всего лишь основанием для сглаживания перехода между цветом звезды и цветом остальной поверхности шара. Для этого используется функция smoothstep, устанавливающая расстояние в 0, если вычисленное расстояние меньше -FWidth, в 1, если вычисленное расстояние больше FWidth, и в ровно интерполированное значение между 0 и 1, если вычисленное расстояние находится между этими двумя значениями. Определив distance как vec4, эти вычисления можно производить над четырьмя значениями параллельно, smoothstep выполняет операцию деления, и так как FWidth является значением типа fl oat, нужно выполнить всего одну операцию:
distance -= smoothstepf-FWidtft, FWidtb. distance);
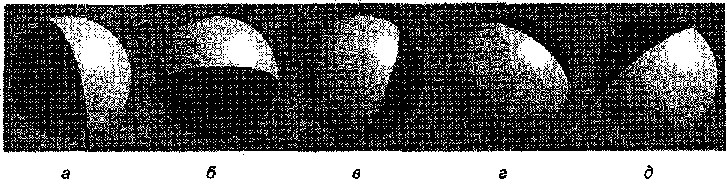
Рис. 11.1. Результаты вычисления принадлежности точек полупространству (ATI Research, Inc.)
Теперь можно быстро добавлять значения в distance, выполняя операцию dot над di stance и vec4, содержащим все единицы;
