Усреднение функций цветового соответствия
В конце 20-х годов прошлого века были выполнены две серии экспериментов по усреднению функций цветового соответствия, которые провели Райт (1928-29), использовавший монохроматические кардинальные стимулы, и Гилд (1931), использовавший широкополосные кардинальные стимулы.
Поскольку кардинальные стимулы первого эксперимента могут быть описаны с помощью трехстимульных значений кардинальных стимулов второго эксперимента, то возможно выполнить линейное (3х3-матричное) преобразование, конвертирующее трехстимульные значения из одной системы в другую. Благодаря тому, что преобразование с успехом применимо к функциям цветового соответствия (поскольку они представляют собой набор самостоятельных трехстимульных значений), было выполнено преобразование, объединяющее данные Райта и Гилда в общий набор кардинальных стимулов.
Эксперименты Райта и Гилда оказались исключительно хорошо согласованными и подтвердили теоретические предположения, касающиеся получения и использования функций цветового соответствия, поэтому CIE решила установить стандартный набор функций цветового соответствия, основанный на усредненных результатах обоих экспериментов. Затем полученные функции были преобразованы в функции для набора узкополосных кардинальных стимулов с длинами волн 700.0нм, 546.1 нми435.8нм соответственно (рис. 3.7).
Затем CIE решила выполнить преобразование полученных функций к функциям для еще одного набора кардинальных стимулов - XKZ; основной предпосылкой к этому преобразованию было стремление устранить отрицательные значения из функций цветового соответствия и принудительно уравнять одну из этих функций с функцией фотопической световой эффективности F(X) CIE 1924.
Отрицательные значения были удалены за счет создания такого набора кардинальных стимулов, с помощью которого можно было бы уравнять все физически воспроизводимые цветовые стимулы. Такими кардинальными стимулами оказались лишь воображаемые кардинальные стимулы, более насыщенные, чем монохроматический свет, и их получение - это математическая абстракция. Нужно отметить, что, несмотря на то, что кардинальные стимулы условны, функции цветового соответствия, полученные с такими кардинальными стимулами, основаны на совершенно реальных результатах цветового уравнивания и подчиняются грассмановским законам.
Принудительное уравнивание одной из функций цветового соответствия
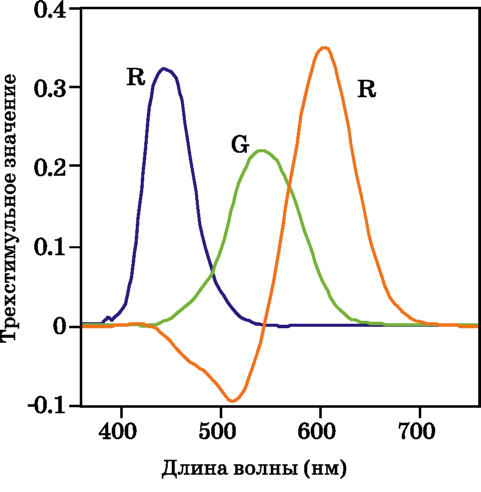
Рис. 3.7 Спектральные трехстимульные значения для колориметрической системы CIE RGB с монохроматическими кардинальными стимулами 435.8, 546.1 и 700.0 нм.
с функцией F(X) выполнено с целью внедрения фотометрической системы CIE (принята в 1924 г.) в колориметрическую систему CIE (принята в 1931 г.). Поступили так: воображаемым кардинальным стимулам Xи Z был адресован сугубо «неяркостный» ответ, а вся полнота яркостного ответа адресована стимулу У Функции цветового соответствия для кардинальных стимулов X.YZ, - это x(X),y(X),z(k) соответственно, которые именуются как «функции цветового соответствия стандартного колориметрического наблюдателя CIE 1931». Табличное представление этих функций дано в таблице 3.3, а графическое - на рис. 3.8 в значимом для нас диапазоне длин волн (360-760 нм с шагом 5 нм). (CIE позиционирует функции цветового соответствия в диапазоне от 360 до 830 нм с шагом 1 нм и с множеством десятичных знаков после запятой).
