Урок 30. Определение столкновений и моделирование законов физики

Исходный код на котором основан этот урок, взят из моей старой конкурсной работы (ее можно найти на OGLchallenge.dhs.org). Тема называлась “Сумасшедшие столкновения” и моя статья (которая, кстати, заняла первое место :)) была названа Магической Комнатой. Она освещала определение столкновений, моделирование законов физики и эффекты.

 

Определение столкновений

Трудная тема, и честно говоря, я не знаю до сих пор простых подходов для ее решения. Для каждого приложения существуют различные способы нахождения и проверки столкновений. Конечно, существуют обобщенные физические законы и они могут работать с любыми видами объектов, но они очень медленные.

Мы собираемся исследовать алгоритмы, которые очень быстрые, легкие для понимания и до некоторой степени гибкие. К тому же важно и должно быть рассмотрено, что сделать, когда столкновение определено, и то, как тогда перемещать объекты, в соответствии с законами физики. Мы имеет много материала для рассмотрения. Давайте просмотрим, что мы собираемся изучить:

1) Определение столкновений

·         Движущаяся сфера - Плоскость

·         Движущаяся сфера - Цилиндр

·         Движущаяся сфера - движущаяся сфера

 

2) Моделирование законов физики

·         Реакция на столкновение

·         Движение под действием гравитации с использованием уравнения Эйлера

 

3) Специальные эффекты

·         Моделирование взрыва с использованием метода Fin-Tree Billboard

·         Использование звуков с помощью The Windows Multimedia Library (только для Windows)

 

4) Разъяснение кода

·         Код, разделен на 5 файлов

 

В этом коде есть много удобного для дальнейшего использования! Классы операций с векторами, лучами и матрицами очень полезны. Я использую их до сих пор в собственных проектах.

 

1) Определение столкновений.

Для определения столкновений мы собираемся использовать алгоритмы метода трассировки лучей. Дадим сначала определение луча.

Луч задается с помощью вектора, он имеет начальную точку и вектор (обычно нормализованный), по направлению которого идет луч. По существу, луч исходит из начальной точки и движется по направлению направляющего вектора. Итак, наше уравнение луча:

PointOnRay = Raystart + t * Raydirection

t - точка, принимающая значения из [0, бесконечность).

При 0 мы получим начальную точку, используя другие значения, мы получаем соответствующие точки вдоль луча.

PointOnRay, Raystart, Raydirection - трехмерные вектора со значениями (x,y,z). Сейчас мы можем использовать это представление луча и вычислить пересечение с плоскостью или цилиндром.

 

Определение пересечения луча с плоскостью.

Плоскость представляется с помощью векторного представления таким образом:

 

Xn dot X = d

 

Xn, X - векторы, и d - значение с плавающей точкой.

Xn - ее нормаль.

X - точка на ее поверхности.

d - расстояние от центра системы координат до плоскости вдоль нормали.

По существу, плоскость обозначает половину пространства. Поэтому, все, что нам необходимо, чтобы определить плоскость, это 3D точка и нормаль в этой точке, которая является перпендикуляром к этой плоскости. Эти два вектора формируют плоскость, т.е. если мы возьмем для 3D точки вектор (0,0,0) и нормаль (0,1,0), мы по существу определяем плоскость через оси x и y. Поэтому, определения точки и нормали достаточно для вычисления векторного представления плоскости.

Согласно векторному уравнению плоскости, нормаль - Xn и 3D точка из которой исходит нормаль - X. Недостающие значение - d, которое легко вычисляется с помощью dot product (скалярного произведения).

(Замечание: Это векторное представление эквивалентно широко известной параметрической формуле плоскости Ax + By + Cz + D=0, для соответствия надо просто взять три значения нормали x,y,z как A,B,C и присвоить D=-d).

Вот два уравнения, которые мы пока что имеем:

 

PointOnRay = Raystart + t * Raydirection
Xn dot X = d

Если луч пересекает плоскость в некоторой точке, то тогда должна быть какая-то точка на луче, которая соответствует уравнению плоскости следующим образом:

 

Xn dot PointOnRay = d или (Xn dot Raystart) + t * (Xn dot Raydirection) = d

находя для t:

 

t = (d - Xn dot Raystart) / (Xn dot Raydirection)

заменяя d:

 

t= (Xn dot PointOnRay - Xn dot Raystart) / (Xn dot Raydirection)

сокращая его:

 

t= (Xn dot (PointOnRay - Raystart)) / (Xn dot Raydirection)

t представляет расстояние от начала луча до точки пересечения с плоскостью по направлению луча. Поэтому, подставляя t в уравнении луча, мы можем получить точку столкновения. Однако, существует несколько особых случаев. Если Xn dot Raydirection = 0, тогда эти два вектора перпендикулярны (луч идет паралельно плоскости), и столкновения не будет. Если t отрицателен, луч направлен в противоположную от плоскости сторону и не пересекает ее.

 

int TestIntersionPlane

(const Plane& plane,const TVector& position,

const TVector& direction, double& lamda, TVector& pNormal)

{

// Векторное произведение между нормалью плоскости и лучом

double DotProduct=direction.dot(plane._Normal);

double l2;

 

// Определить, параллелен ли луч плоскости

if ((DotProduct<ZERO)&&(DotProduct>-ZERO))

return 0;

 

// Определить расстояние до точки столкновения

l2=(plane._Normal.dot(plane._Position-position))/DotProduct;

 

if (l2<-ZERO) // Определить, пересекает ли луч плоскость

return 0;

 

pNormal=plane._Normal;

lamda=l2;

return 1;

}

Код, приведенный выше, вычисляет и возвращает пересечение. Он возвращает 1, если пересечение есть, иначе 0. Параметры: плоскость (plane), начало (position) и направление вектора луча (direction), lamda - расстояние до точки столкновения, если оно есть, и вычисляется нормаль от точки столкновения (pNormal).

 

Пересечение луча с цилиндром

Вычисление пересечения между бесконечным цилиндром и лучом настолько сложено, что я не хочу объяснять его здесь. Этот способ требует больших математических расчетов и его просто объяснить, но моя главная цель дать вам инструменты, без излишней детализации (это не класс геометрии). Если кто-то интересуется теорией, на которой основан код, смотрите Graphic Gems II Book (pp 35, intersection of a with a cylinder). Цилиндр представляется как луч, с началом и направляющим вектором (здесь он совпадает с как осью), и радиус (радиус вокруг оси цилиндра). Соответственно функция:

 

int TestIntersionCylinder

(const Cylinder& cylinder, const TVector& position, const TVector& direction,

double& lamda, TVector& pNormal, TVector& newposition)

  Возвращает 1, если было обнаружено пересечение, иначе 0.

Параметры: структура, задающая цилиндр (смотрите в объяснении кода ниже), вектор начала и вектор направления луча. Значения, возвращаемые через параметры - расстояние, нормаль от точки пересечения и сама точка пересечения.

Столкновение сферы со сферой

Сфера задается с помощью ее центра и ее радиуса. Столкновение двух сфер определить легко. Находя расстояние между двумя центрами (метод dist класса TVector) мы можем это определить, пересекаются ли они, если расстояние меньше, чем сумма их радиусов.

Проблема лежит в определении, столкнуться ли две ДВИЖУЩИЕСЯ сферы. Ниже есть пример, где две сферы двигаются в течение временного шага из одной точки в другую. Их пути пересекаются, но этого недостаточно, чтобы подтвердить, что столкновение произошло (они могут пройти в различное время), да и точку столкновения определить невозможно.

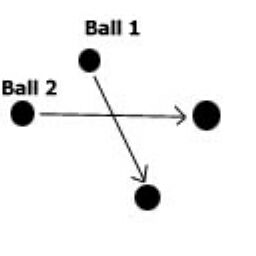
Рисунок 1

Предыдущие методы пересечения были решением уравнений объектов для определения пересечения. Когда используются сложные формы объектов или эти уравнения не применимы или не могут быть решены, должны быть использованы другие методы. Начальные и конечные точки, временной шаг, скорость (направление сферы + скорость) сферы и метод вычисления пересечения неподвижных сфер уже известны. Чтобы вычислить пересечение, временной шаг должен быть разрезан на более мелкие части. Затем, мы перемещаем сферы в соответствии к этим разрезанным временным шагам, используя ее скорость, и проверяем столкновение. Если в какой-либо точке обнаруживается столкновение (это означает, что сферы уже проникли друг в друга), то мы берем предыдущую позицию как точку пересечения (мы можем начать интерполяцию между этими точками, чтобы точно определить позицию пересечения, но это в основном не требуется).

Чем меньше временной шаг, чем больше частей мы используем, тем точнее метод. Например, допустим временной шаг равен 1 и количество частей - 3. Мы бы проверили два шара на столкновение во время 0, 0.33, 0.66, 1. Легко!!!!

Код, который это выполняет:

 

/*** Определить, какой из текущих шаров ***/

/*** пересекает другой в текущем временном шаге ***/

/*** Возвращает индекс двух пересекающихся шаров, точку и время пересечения ***/

 

int FindBallCol

(TVector& point, double& TimePoint, double Time2,

int& BallNr1, int& BallNr2)

{

TVector RelativeV;

TRay rays;

double MyTime=0.0, Add=Time2/150.0, Timedummy=10000, Timedummy2=-1;

TVector posi;

// Проверка всех шаров один относительно других за 150 маленьких шагов

for (int i=0;i<NrOfBalls-1;i++)

{

for (int j=i+1;j<NrOfBalls;j++)

{

RelativeV=ArrayVel[i]-ArrayVel[j]; // Найти расстояние

rays=TRay(OldPos[i],TVector::unit(RelativeV));

MyTime=0.0;

 

// Если расстояние между центрами больше чем 2*радиус

if ( (rays.dist(OldPos[j])) > 40) continue;

// Произошло пересечение

// Цикл для точного определения точки пересечения

while (MyTime<Time2)

{

MyTime+=Add;

posi=OldPos[i]+RelativeV*MyTime;

if (posi.dist(OldPos[j])<=40)

{

point=posi;

if (Timedummy>(MyTime-Add)) Timedummy=MyTime-Add;

BallNr1=i;

BallNr2=j;

break;

}

}

}

}

 

if (Timedummy!=10000)

{

TimePoint=Timedummy;

return 1;

}

return 0;

}

 

Как использовать то, что мы только что изучили.

Поскольку сейчас мы можем определить точку пересечения между лучом и плоскостью/цилиндром, мы должны использовать это каким-нибудь образом для определения столкновения между сферой и одним из этих примитивов. Что мы могли сделать до этого, это определить точную точку столкновения между частицей (точкой) и плоскостью/цилиндром. Начало луча - расположение частицы, и направление луча - его вектор скорости (скорость и направление). Сделать это применительно к сферам довольно легко. Смотрите на рисунке 2а, как это может быть выполнено.

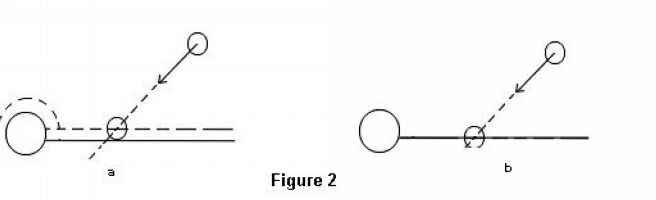
Рисунок 2a                                         Рисунок 2b

Каждая сфера имеет радиус, берем центр сферы как частицу (точка) и сдвигаем поверхность вдоль нормали каждой интересующей нас плоскости/цилиндра. На рисунке 2а эти новые примитивы изображены пунктирными линиями. Наши настоящие примитивы изображены непрерывными линиями, но тест на столкновение делается с помощью сдвинутых примитивов (представленных пунктирными линиями). Фактически, мы выполняем тест на пересечение с помощью небольшой плоскости сдвига и увеличенным радиусом цилиндра. Используя эту маленькую хитрость, шар не проникает в поверхность, если пересечение обнаружено с помощью его центра. Иначе мы получаем ситуацию как на рисунке 2b, где сфера проникает в поверхность. Это происходит, потому что мы определяем пересечение между его центром и примитивом, что означает, что мы не изменяли наш первоначальный код!

Определив, где будет столкновение, мы должны определить, будет ли пересечение в нашем текущем временном шаге. Временной шаг это время, в течение которого мы перемещаем сферу из ее текущей точки в соответствии с ее скоростью. Из-за того, что мы тестируем с помощью бесконечных лучей, всегда существует возможность того, что точка столкновения будет позади нового расположения сферы. Чтобы определить это, мы перемещаем сферу, вычисляем ее новое расположение и находим расстояние между начальной и конечной точкой. Из нашей процедуры определения столкновений мы также можем взять расстояния от начальной точки до точки столкновения. Если это расстояние меньше чем расстояние между начальной и конечной точкой, тогда столкновение есть. Чтобы вычислить точное время, мы решаем следующее простое уравнение. Представляем расстояние между начальной и конечной точкой как Dst, расстояние между начальной точкой и точкой столкновения - Dsc, и временной шаг - Т. Время, когда происходит столкновение (Тс):

Tc= Dsc*T / Dst

Все это выполняется, конечно, если пересечение было определено. Возвращаемое время - часть от целого временного шага, если временной шаг был в 1 секунду, и мы обнаружили пересечение точно в середине расстояния, то вычисленное время столкновения будет 0.5 сек. Сейчас точка пересечения может быть вычислена только умножением Тс на текущую скорость и прибавлением к начальной точке.

Collision point= Start + Velocity*Tc

Это точка столкновения на расширенном примитиве, чтобы найти точку столкновения на настоящем примитиве мы добавляем к этой точке реверс нормали от этой точки (который также возвращается процедурой пересечения) с помощью радиуса сферы. Заметьте, что процедура пересечения цилиндра возвращает точку пересечения, если она существует, поэтому не нуждается в вычислении.

 

2) Моделирование законов физики

Реакция на столкновения

Определить, как отреагируют после удара неподвижные объекты, типа плоскостей, цилиндров также важно, как определить точку столкновения. Используя описанные алгоритмы и функции, можно обнаружить точную точку столкновения, нормаль от нее и время внутри временного шага, в течение которого происходит столкновение.

Чтобы определить, как отреагировать на столкновение, должны быть применены законы физики. Когда объект сталкивается с поверхностью, его направление меняется, т.е. он отскакивает. Угол нового направления (или вектор отражения) от нормали точки столкновения такой же, как у первоначального вектора. Рисунок 3 показывает столкновение со сферой.

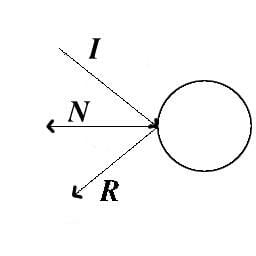
Рисунок 3

R - новый направляющий вектор

I - старый направляющий вектор, до столкновения

N - нормаль от точки столкновения

Новый вектор R вычисляется следующим образом:

R= 2*(-I dot N)*N + I

Есть ограничение: вектора I и N должны быть единичными векторами. Вектор скорости, который мы использовали в наших примерах, представляет скорость и направление. Вектор скорости не может быть включен в уравнение за место I, без преобразования. Скорость должна быть исключена. Скорость исключается нахождением величины вектора. Когда величина вектора найдена, вектор может быть преобразован в единичный и включен в уравнение, вычисляющее вектор отражения R. R показывает нам направление луча отражения, но для того, чтобы использовать как вектор скорости, необходимо к нему подключить скорость. Берем его, умножаем на величину первоначального луча, получаем правильный вектор скорости.

В примере эта процедура применяется для вычисления реакции на столкновение, когда шар сталкивается с плоскостью или цилиндром. Но она работает также для любых поверхностей, их форма не имеет значения. Пока точка столкновения и нормаль могут быть вычислены, метод вычисления реакции на столкновение всегда будет тот же самый. Код, который выполняет эти операции:

 

rt2=ArrayVel[BallNr].mag(); // Найти величину скорости

ArrayVel[BallNr].unit(); // Нормализовать его

 

// Вычислить отражение

ArrayVel[BallNr]=TVector::unit( (normal*(2*normal.dot(-ArrayVel[BallNr]))) + ArrayVel[BallNr] );

// Умножить на величину скорости для получения вектора скорости

ArrayVel[BallNr]=ArrayVel[BallNr]*rt2;

 

Когда сфера сталкивается с другой сферой

Определить реакцию на столкновение двух шаров намного труднее. Должны быть решены сложные уравнения динамики частиц, и поэтому я выдам только окончательное решение без каких-либо доказательств. Просто поверьте мне в этом :). Во время столкновения имеем ситуацию, как изображено на рисунке 4.

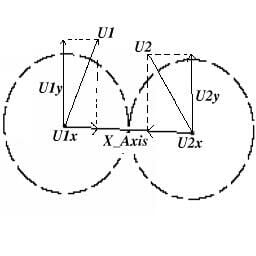
Рисунок 4

 

U1 и U2 векторы скорости двух сфер во время столкновения. Существует ось (X_Axis), вектор, которые соединяет центры двух сфер, и U1x, U2x проекции векторов скоростей U1,U2 ось (X_Axis).

U1y и U2y проекции векторов скорости U1,U2 на ось, перпендикулярную X_Axis. Чтобы найти эти вектора нужно просто произвести скалярное произведение. M1, M2 - массы двух сфер, соответственно. V1,V2 - новые скорости после столкновения, и V1x, V1y, V2x, V2y - проекции векторов скорости на X_Axis.

Более подробно:

a) Найти X_Axis

X_Axis = (center2 - center1);

Unify X_Axis, X_Axis.unit();

b) Найти проекции

U1x= X_Axis * (X_Axis dot U1)

U1y= U1 - U1x

U2x =-X_Axis * (-X_Axis dot U2)

U2y =U2 - U2x

c) Найти новые скорости

(U1x * M1)+(U2x*M2)-(U1x-U2x)*M2

V1x= --------------------------------

M1+M2

(U1x * M1)+(U2x*M2)-(U2x-U1x)*M1

V2x= --------------------------------

M1+M2

В нашем приложении мы установили M1=M2=1, поэтому уравнение получилось даже проще.

d) Найти окончательные скорости

V1y=U1y
V2y=U2y
V1=V1x+V1y
V2=V2x+V2y

Решение этих уравнений требует много работы, но раз они в той форме, как выше, они могут быть использованы совершенно легко. Код, который вычисляет действительную реакцию на столкновение:

 

TVector pb1,pb2,xaxis,U1x,U1y,U2x,U2y,V1x,V1y,V2x,V2y;

double a,b;

// Найти расположение первого шара

pb1=OldPos[BallColNr1]+ArrayVel[BallColNr1]*BallTime;

// Найти расположение второго шара

pb2=OldPos[BallColNr2]+ArrayVel[BallColNr2]*BallTime;

xaxis=(pb2-pb1).unit(); // Найти X-Axis

a=xaxis.dot(ArrayVel[BallColNr1]); // Найти проекцию

U1x=xaxis*a; // Найти спроецированные вектора

U1y=ArrayVel[BallColNr1]-U1x;

xaxis=(pb1-pb2).unit(); // Сделать также, как выше

b=xaxis.dot(ArrayVel[BallColNr2]); // Найти проекцию

U2x=xaxis*b; // Векторы для другого шара

U2y=ArrayVel[BallColNr2]-U2x;

V1x=(U1x+U2x-(U1x-U2x))*0.5; // Сейчас найти новые скорости

V2x=(U1x+U2x-(U2x-U1x))*0.5;

V1y=U1y;

V2y=U2y;

for (j=0;j<NrOfBalls;j++) // Обновить все новые расположения

ArrayPos[j]=OldPos[j]+ArrayVel[j]*BallTime;

ArrayVel[BallColNr1]=V1x+V1y; // Установить новые вектора скорости

ArrayVel[BallColNr2]=V2x+V2y; // столкнувшимся шарам

 

Движение под действием гравитации, с использованием уравнения Эйлера

Чтобы изобразить реалистичное движение со столкновениями, определение точки столкновения и вычисления реакции не достаточно. Движение основывается на физических законах и тоже должно быть смоделировано.

Наиболее широко используемый метод для этого - использование уравнения Эйлера. Как показано, все вычисления должны быть выполнены с использованием временного шага. Это означает, что все моделирование происходит в некоторых временных шагах, в течение которых происходит движение, и выполняются тесты на столкновения и реакцию. Как пример, мы можем произвести моделирование в течение 2 секунд на каждом фрейме. Основываясь на уравнении Эйлера, скорость и расположение в каждом нового временном шаге вычисляется следующим образом:

Velocity_New = Velovity_Old + Acceleration*TimeStep
Position_New = Position_Old + Velocity_New*TimeStep

Сейчас объекты перемещаются и тестируются на столкновения, используя новую скорость. Ускорение для каждого объекта вычисляется делением силы, действующей на него, на его массу, в соответствии с эти уравнением:

Force = mass * acceleration

Много физических формул :)

Но, в нашем случае, на объекты действует только сила тяжести, которая может быть представлена сейчас как вектор, указывающий ускорение. В нашем случае, что-либо отрицательное в направлении Y, типа (0,-0.5,0). Это означает, что в начале каждого временного шага, мы вычисляем новую скорость каждой сферы и перемещаем их, тестируя на столкновение. Если во время временного шага происходит столкновение (скажем после 0.5 сек. с временным шагом равным 1 сек.) мы передвигаем объект в эту позицию, вычисляем отражение (новый вектор скорости) и перемещаем объект за оставшееся время (0.5 в нашем примере) снова тестируя на столкновения в течение этого времени. Эта процедура выполняется пока не завершится временной шаг.

Когда присутствует много движущихся объектов, каждый движущийся объект тестируется на пересечение с неподвижными объектами и ближайшее пересечение записывается. Далее выполняется тест на пересечение среди движущихся объектов для определения столкновений, в котором каждый объект тестируется с каждым другим. Обнаруженные пересечения сравниваются с пересечениями со статическим объектами, и берется наиболее близкое из них. Все моделирование обновляется в этой точке, (т.е., если ближайшее пересечение было после 0.5 сек., мы должны переместить все объекты на 0.5 сек.), для столкнувшихся объектов вычисляется вектор отражения, и цикл снова выполняется за оставшееся время.

 

3) Специальные эффекты

Взрывы

Каждый раз, когда происходит столкновение, в точке столкновения происходит взрыв. Хороший способ моделировать взрывы - произвести смешивание двух перпендикулярных друг другу полигонов с центрами в интересующей точке (в точке пересечения). Полигоны уменьшаются и исчезают со временем. Исчезновение выполняется изменением для вершин в течение времени значения alpha от 1 до 0. Так как возникает много полупрозрачных полигонов, то это может вызвать проблемы, и они могут перекрывать друг друга (как указано в Red Book в главе о прозрачности и смешивании) из-за Z-буфера, мы заимствуем технику, используемую в рендеринге частиц. Чтобы реализовать корректно этот трюк (как это описано в Red Book), мы должны отсортировать полигоны в соответствии с их расположением по глубине, но с выключением записи в буфер глубины (не чтения). Заметьте, что число взрывов ограничено до 20 за один фрейм, если происходят дополнительные взрывы, буфер переполняется, и они сбрасываются. Код, который производит взрывы:

 

// Исполнение / смешивание взрывов

glEnable(GL_BLEND); // Включить смешивание

glDepthMask(GL_FALSE); // Отключить запись буфера глубины

glBindTexture(GL_TEXTURE_2D, texture[1]); // Подключение текстуры

for(i=0; i<20; i++) // Обновление и визуализация взрывов

{

if(ExplosionArray[i]._Alpha>=0)

{

glPushMatrix();

ExplosionArray[i]._Alpha-=0.01f; // Обновить альфу

ExplosionArray[i]._Scale+=0.03f; // Обновить размер

// Назначить прозрачным вершинам желтый цвет

glColor4f(1,1,0,ExplosionArray[i]._Alpha); // Размер

glScalef(ExplosionArray[i]._Scale,

ExplosionArray[i]._Scale,ExplosionArray[i]._Scale);

// Переместить в позицию с учетом масштабирования

glTranslatef(

(float)ExplosionArray[i]._Position.X()/ExplosionArray[i]._Scale,

(float)ExplosionArray[i]._Position.Y()/ExplosionArray[i]._Scale,

(float)ExplosionArray[i]._Position.Z()/ExplosionArray[i]._Scale);

glCallList(dlist);// Вызвать список изображений

glPopMatrix();

}

}

 

Звук

Для звука была использована мультимедийная функция окошек PlaySound(). Это быстрый и отвратительный способ проигрывания звуковых файлов быстро и без хлопот.

 

4) Разъяснение кода

Поздравляю…

Если вы еще со мной, значит, вы успешно пережили теоретическую часть ;). Перед тем как позабавиться с демкой, необходимы некоторые разъяснения исходного кода. Основные действия и шаги моделирования следующие (в псевдокоде):

Цикл (ВременнойШаг!=0)
{
      Цикл по всем шарам
      {
           вычислить ближайшее столкновение с плоскостью
           вычислить ближайшее столкновение с цилиндром
           Сохранить и заменить, если это ближайшее пересечение
           по времени вычисленное до сих пор;
      }
      Проверить на столкновение среди движущихся шаров;
      Сохранить и заменить, если это ближайшее пересечение
      по времени, вычисленное до сих пор;
     If (Столкновение произошло)
      {
           Переместить все шары на время, равное времени столкновения;
           (Мы уже вычислили точку, нормаль и время столкновения.)
           Вычислить реакцию;
           ВременнойШаг -=ВремяСтолкновения;
      }
      else
           Переместить все шары на время, равное временному шагу
}

Настоящий код, выполняющий псевдокод выше - тяжелей для чтения, но, в сущности, точная реализация этого псевдокода. 

// Пока не закончится временной шаг

while (RestTime>ZERO)

{

lamda=10000; // Инициализировать очень большое значение

// Для всех шаров найти ближайщее пересечение между шарами и плоскостями/цилиндрами

for (int i=0;i<NrOfBalls;i++)

{

// Вычислить новое расположение и расстояние

OldPos[i]=ArrayPos[i];

TVector::unit(ArrayVel[i],uveloc);

ArrayPos[i]=ArrayPos[i]+ArrayVel[i]*RestTime;

rt2=OldPos[i].dist(ArrayPos[i]);

// Проверить, произошло ли столкновение между шаром и всеми 5 плоскостями

if (TestIntersionPlane(pl1,OldPos[i],uveloc,rt,norm))

{

// Найти время пересечения

rt4=rt*RestTime/rt2;

// Если оно меньше, чем уже сохраненное во временном шаге, заменить

if (rt4<=lamda)

{

// Если время пересечения в текущем временном шаге

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=OldPos[i]+uveloc*rt;

lamda=rt4;

BallNr=i;

}

}

}

 

if (TestIntersionPlane(pl2,OldPos[i],uveloc,rt,norm))

{

 

// …То же самое, что и выше

}

 

if (TestIntersionPlane(pl3,OldPos[i],uveloc,rt,norm))

{

 

// …То же самое, что и выше

}

 

if (TestIntersionPlane(pl4,OldPos[i],uveloc,rt,norm))

{

 

// …То же самое, что и выше

}

 

if (TestIntersionPlane(pl5,OldPos[i],uveloc,rt,norm))

{

 

// …То же самое, что и выше

}

 

// Сейчас проверяем пересечения с 3 цилиндрами

if (TestIntersionCylinder(cyl1,OldPos[i],uveloc,rt,norm,Nc))

{

rt4=rt*RestTime/rt2;

if (rt4<=lamda)

{

if (rt4<=RestTime+ZERO)

if (! ((rt<=ZERO)&&(uveloc.dot(norm)>ZERO)) )

{

normal=norm;

point=Nc;

lamda=rt4;

BallNr=i;

}

}

}

 

if (TestIntersionCylinder(cyl2,OldPos[i],uveloc,rt,norm,Nc))

{

// …То же самое, что и выше

}

 

if (TestIntersionCylinder(cyl3,OldPos[i],uveloc,rt,norm,Nc))

{

// …То же самое, что и выше

}

 

}

 

// После того, как были проверены все шары на столкновение с плоскостями/цилиндрами

// Проверить между ними и записать наименьшее время столкновения

if (FindBallCol(Pos2,BallTime,RestTime,BallColNr1,BallColNr2))

{

if (sounds)

PlaySound("Explode.wav",NULL,SND_FILENAME|SND_ASYNC);

 

if ( (lamda==10000) || (lamda>BallTime) )

{

RestTime=RestTime-BallTime;

TVector pb1,pb2,xaxis,U1x,U1y,U2x,U2y,V1x,V1y,V2x,V2y;

double a,b;

.

.

Код опущен для экономии пространства

Код описан в разделе Моделирование физических законов

Столкновение между сферами

.

.

//Обновить массив взрывов и вставить взрыв

for(j=0;j<20;j++)

{

if (ExplosionArray[j]._Alpha<=0)

{

ExplosionArray[j]._Alpha=1;

ExplosionArray[j]._Position=ArrayPos[BallColNr1];

ExplosionArray[j]._Scale=1;

break;

}

}

 

continue;

}

}

 

// Конец проверок

// Если столкновение произошло, произвести моделирование для точного временного шага

// и вычислить реакцию для столкнувшихся шаров

if (lamda!=10000)

{

RestTime-=lamda;

for (j=0;j<NrOfBalls;j++)

ArrayPos[j]=OldPos[j]+ArrayVel[j]*lamda;

rt2=ArrayVel[BallNr].mag();

ArrayVel[BallNr].unit();

ArrayVel[BallNr]=TVector::unit( (normal*(2*normal.dot(-ArrayVel[BallNr])))

+ ArrayVel[BallNr] );

ArrayVel[BallNr]=ArrayVel[BallNr]*rt2;

 

// Обновить массив взрывов и вставить взрыв

for(j=0;j<20;j++)

{

if (ExplosionArray[j]._Alpha<=0)

{

ExplosionArray[j]._Alpha=1;

ExplosionArray[j]._Position=point;

ExplosionArray[j]._Scale=1;

break;

}

}

}

else RestTime=0;

}

 

Основные глобальные переменные, представляющие важность:

 

Основные интересующие функции:

 

  Для большей информации смотрите исходный код. Я пытался прокомментировать его настолько хорошо, насколько смог. Сейчас, когда логика определения столкновения и реакции понята, исходный код должен стать ясным. Не стесняйтесь обращаться ко мне для получения большей информации.

Как я заявил в начале этого учебника, тема определения столкновений - очень сложная тема, чтобы ее охватить в одном учебнике. Вы многое изучите в этом учебнике, достаточное для создания своих собственных достаточно впечатляющих демок, но все еще есть много чего, что нужно изучить по этой теме. Сейчас, когда вы имеете основы, все другие исходники по определению столкновений и моделированию физических законов должны стать легче для понимания. С этими словами, я отправляю вас своей дорогой и желаю вам счастливых столкновений!!!

Немного информации о Dimitrios Christopoulos: в настоящее время он работает как программный инженер по виртуальной реальности в Foundation of the Hellenic World в Athens/Греция (www.fhw.gr). Хотя он родился в Германии, он учился в Греции в University of Patras на факультете Компьютерной инженерии и информатики. Он также имеет MSc степень в Университете Hull (UK) по Компьютерной Графике и Виртуальному окружению. Первые шаги по программированию игр он начинал на Basic на Commodore 64, и перешел на C/C++/Assembly на PC платформе, после того как стал студентом. В течение нескольких последних лет он перешел на OpenGL. Также смотри на его сайте http://members.xoom.com/D_Christop.

 

© Dimitrios Christopoulos

 21 декабря 2001 (c)  Владимир Намхоев