Урок 28. Фрагменты поверхностей Безье.
В этом уроке пойдет речь о поверхностях Безье, и я буду надеяться, что кто-то, прочитав этот урок, покажет нам более интересные варианты использования их, чем я. Здесь не пойдет речь о библиотеке фрагментов поверхностей Безье (Bezier patch, или патчи Безье, или лоскуты Безье), а скорее я попытаюсь ознакомить вас концепцией того, как реально эти кривые поверхности работают. Так как это, скорее всего не формальное изложение, то я иногда делаю небольшие отступления от формальной терминологии, для лучшего понимания сути дела. Я надеюсь, что это поможет. Если вы уже знакомы с Безье, и вы читаете эту статью, что бы посмотреть что я тут накрутил, то позор Вам! Но, если я действительно где-то ошибся, сообщите мне об этой ошибке или NeHe, в конце концов, никто не совершенен. И еще одно, код в уроке не оптимизирован, в противоположность моей обычной практики, это потому что я хочу дать всем возможность точно понять, как это работает. Отлично, хватит вводных слов, смотрите!
Математика — дьявольская музыка:: (предупреждаю, вероятно, это длинная секция)
Отлично, Вам будет очень трудно понять поверхности Безье без минимума математики, стоящей за этим, однако, если Вы не чувствуете в себе сил и желания читать эту секцию, или Вы уже знакомы с этой математикой, Вы можете опустить ее. Вначале мы займемся кривыми Безье, затем рассмотрим фрагменты Безье.
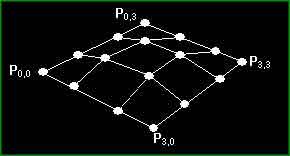
Даже, если Вы не знакомы ранее с таким термином, как кривые Безье, но работали в каком-нибудь редакторе графики (например, CorelDraw), то, скорее всего Вы знакомы с кривыми Безье, пусть даже и не под таким названием. Так как это основной метод рисования кривых линий. Обыкновенно для работы этого метода необходимо четыре точки, при чем две точки, изображают касательные, которые идут слева и справа. Вот как это выглядит:

Из разных форм представления кривой Безье — это наиболее простая (удлинять кривые можно присоединяя их друг к другу (много раз без вмешательства пользователя)). Эта кривая обычно задается только четырьмя точками: двумя концевыми контрольными точками и двумя средними контрольными точками. Для компьютера все точки идентичны, но для упрощения работы пользователя мы часто соединяем первые и последние две, соответственно, поскольку эти линии всегда будут касательными к конечной точке. Этот тип кривых задается параметрически и рисуется при помощи нахождения заданного числа равноотстоящих друг от друга точек на кривой и последующего их соединения прямыми линями. Таким образом, мы может контролировать разрешение фрагмента (patch) и скорость вычислений. Наиболее стандартный способ использовать это при тесселяции (разбиении), т.е. уменьшать количество разбиений поверхности при большом удалении от камеры и увеличивать количество разбиений при приближении к наблюдателю, чтобы изогнутая поверхность всегда была гладкой и при этом скорость вывода была наилучшей.
Кривые Безье базируются на простой функции, из которой получаются более сложные версии. Вот эта функция:
t + (1 - t) = 1
Не правда ли выглядит удивительно просто? Это действительно Безье, вернее наиболее простая кривая Безье, кривая первой степени. Как можно догадаться из последней фразы, кривые Безье — это полиномы, и как мы помним из алгебры, полином первой степени — это всего лишь прямая линия; что не очень интересно для нас. Хорошо, поскольку это простая функция истинна для всех значений t, мы можем взять квадрат, куб, любую степень этого выражения с обеих сторон, и это все еще будет истиной? Отлично, давайте попробуем кубическую степень.
(t + (1-t))^3 = 1^3
t^3 + 3*t^2*(1-t) + 3*t*(1-t)^2 + (1-t)^3 = 1
Это уравнение мы и будем использовать для вычисления наиболее общей кривой Безье третьей степени. Это наиболее общее уравнение по двум причинам: a) это полином с наиболее низкой степенью, который не обязательно должен лежать в плоскости (есть четыре контрольных точки) и b) касательные линии к сторонам не зависят одна от другой (в полиноме со второй степенью есть только три контрольных точки). Поэтому вы уже видите кривую Безье? Хе-хе, по мне так ни то ни другое, так как я должен добавить еще кое-что.
Отлично, так как с левой стороны стоит единица, то можно предположить, что когда мы сложим все компоненты, то они все еще будут равны единице. Это похоже на то, что можно описать, как много каждой контрольной точки будет использоваться для вычисления точки кривой? (Подсказка: скажите да ;)). Хорошо Вы правы! Когда мы хотим вычислить значение точки находящейся на кривой, мы просто умножаем каждую компоненту уравнения на свою контрольную точку (как вектор) и находим сумму. Вообще, мы работаем с 0 <= t <= 1, но это технически не обязательно. Непонятно? Вот эта функция.
P1*t^3 + P2*3*t^2*(1-t) + P3*3*t*(1-t)^2 +
P4*(1-t)^3 = Pnew
Поскольку полиномы всегда непрерывны, это хороший способ сделать
морфинг между 4 точками. Хотя фактически достижимы (интерполируются) только
точки P1 и P4, когда t = 1 и t
=0, соответственно. Точки P2 и P3 только аппроксимируются, т.е.
кривая проходит рядом с ними, но не через них.
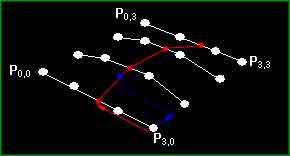
Теперь все прекрасно, но как я могу это использовать в 3D? Хорошо, довольно просто дальше сформировать фрагмент Безье. Для этого нам надо 16 контрольных точек (4*4), и две переменные t и v. Далее вы вычисляете точки v вдоль 4 параллельных кривых, затем используете эти 4 точки для создания новой кривой и вычисления t вдоль этой кривой. Вычисляя нужное количество этих точек, мы можем нарисовать треугольную полоску для соединения их, таким образом, рисуя фрагмент Безье. (Примечание переводчика. Так как каждая концевая точка четырехугольника фрагмента относится к двум сторонам, то всего для их представления надо 8 точек. Затем надо по две контрольные точки на каждую сторону для формирования кривых Безье на этих сторонах. Вначале надо вычислить кривую Безье на одной стороне четырехугольника, затем надо вычислить следующую параллельную ей кривую Безье и так далее. Конечно, для формирования полосок из треугольников необходимо иметь две кривые и рисовать полоски между ними.)
Хорошо, я думаю, пока хватит математики, давайте посмотрим код!
#include <windows.h> // Заголовочный файл для Windows
#include <math.h> // Заголовочный файл для математической библиотеки
#include <stdio.h> // Заголовочный файл для стандартного ввода/вывода
#include <stdlib.h> // Заголовочный файл для стандартной библиотеки
#include <gl\gl.h> // Заголовочный файл для библиотеки OpenGL32
#include <gl\glu.h> // Заголовочный файл для библиотеки GLu32
#include <gl\glaux.h> // Заголовочный файл для GLaux библиотеки
typedef struct point_3d { // Структура для 3D точки( НОВОЕ )
double x, y, z;
} POINT_3D;
typedef struct bpatch { // Структура для полинома фрагмента Безье 3 степени (НОВОЕ)
POINT_3D anchors[4][4]; // Сетка 4x4 анкерных (anchor) точек
GLuint dlBPatch; // Список для фрагмента Безье
GLuint texture; // Текстура для фрагмента
} BEZIER_PATCH;
HDC hDC=NULL; // Контекст устройства
HGLRC hRC=NULL; // Контекст визуализации
HWND hWnd=NULL; // Дескриптор окна
HINSTANCE hInstance; // Экземпляр приложения
bool keys[256]; // Массив для работы с клавиатурой
bool active=TRUE; // Флаг активности приложения
bool fullscreen=TRUE; // Флаг полноэкранного режима
DEVMODE DMsaved; // Сохранить настройки предыдущего режима ( НОВОЕ )
GLfloat rotz = 0.0f; // Вращение по оси Z
BEZIER_PATCH mybezier; // Фрагмент Безье для использования ( НОВОЕ )
BOOL showCPoints=TRUE;// Переключатель отображения контрольных точек сетки ( НОВОЕ )
int divs = 7; // Число интерполяции (Контроль разрешения полигона) ( НОВОЕ )
LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM); // Декларация для WndProc
Далее идут несколько функций для оперирования векторами. Если вы фанат C++, то вы может использовать вместо них какой-то класса 3D точки.
// Сложить 2 точки.
POINT_3D pointAdd(POINT_3D p, POINT_3D q) {
p.x += q.x; p.y += q.y; p.z += q.z;
return p;
}
// Умножение точки на константу
POINT_3D pointTimes(double c, POINT_3D p) {
p.x *= c; p.y *= c; p.z *= c;
return p;
}
// Функция для упрощения создания точки
POINT_3D makePoint(double a, double b, double c) {
POINT_3D p;
p.x = a; p.y = b; p.z = c;
return p;
}
Затем идет функция для вычисления полиномов третьей степени (каждый член в уравнении кривой Безье, является одним из так называемых полиномов Берштейна), ей надо передать переменную u и массив из 4 точек p и вычислить точку на кривой. Изменяя u на одинаковые приращения между 0 и 1, мы получим хорошую аппроксимацию кривой.
// Вычисляем полином 3 степени на основании массива из 4 точек
// и переменной u, которая обычно изменяется от 0 до 1
POINT_3D Bernstein(float u, POINT_3D *p) {
POINT_3D a, b, c, d, r;
a = pointTimes(pow(u,3), p[0]);
b = pointTimes(3*pow(u,2)*(1-u), p[1]);
c = pointTimes(3*u*pow((1-u),2), p[2]);
d = pointTimes(pow((1-u),3), p[3]);
r = pointAdd(pointAdd(a, b), pointAdd(c, d));
return r;
}
Эта функция делает львиную долю работы, генерируя все полоски треугольников и сохраняя их в списке отображения. Мы это делаем, для того чтобы не перевычислять фрагмент каждый кадр. Между прочим, вы можете попробовать использовать урок о Морфинге для морфинга контрольных точек фрагмента. При этом получиться интересный эффект сглаженного морфинга с относительно небольшими затратами (вы только делает морфинг 16 точек, но вы должны перевычислить их). Массив "last" используется для сохранения предыдущей линии точек (поскольку для треугольных полосок необходимы обе строки). Также координаты текстуры вычисляются при помощи использования u и v значений в виде процентов (плоское наложение).
Одну вещь мы не делаем — вычисление нормалей для освещения. Когда вы начнете это делать, в общем, вы будете иметь два параметра. Первый параметр, который вы должны найти — это центр каждого треугольника, и затем использовать побитное исчисление и вычисление тангенса обоих осей x и y, затем сделать векторное произведение чтобы получить перпендикуляр к обоим осям, ЗАТЕМ нормализовать вектор и использовать его как нормаль. ИЛИ (это более быстрый путь) вы можете, для того чтобы получить хорошую аппроксимацию, использовать только нормаль треугольника (вычисленную на ваш любимый манер). Я предпочитаю последний способ, так как, по моему мнению, не стоит жертвовать скоростью взамен не большому улучшению реализма.
// Создание списков отображения на основе данных фрагмента
// и числе разбиений
GLuint genBezier(BEZIER_PATCH patch, int divs) {
int u = 0, v;
float py, px, pyold;
GLuint drawlist = glGenLists(1); // Создать список отображения
POINT_3D temp[4];
POINT_3D *last = (POINT_3D*)malloc(sizeof(POINT_3D)*(divs+1));
// Массив точек для отметки первой линии полигонов
if (patch.dlBPatch != NULL) // Удалить старые списки отображения
glDeleteLists(patch.dlBPatch, 1);
temp[0] = patch.anchors[0][3]; // Первая производная кривая (Вдоль оси X)
temp[1] = patch.anchors[1][3];
temp[2] = patch.anchors[2][3];
temp[3] = patch.anchors[3][3];
for (v=0;v<=divs;v++) { // Создание первой линии точек
px = ((float)v)/((float)divs); // Процент вдоль оси Y
// Используем 4 точки из производной кривой для вычисления точек вдоль кривой
last[v] = Bernstein(px, temp);
}
glNewList(drawlist, GL_COMPILE); // Начнем новый список отображения
glBindTexture(GL_TEXTURE_2D, patch.texture); // Присоединим к текстуре
for (u=1;u<=divs;u++) {
py = ((float)u)/((float)divs); // Процент вдоль оси Y
pyold = ((float)u-1.0f)/((float)divs); // Процент вдоль старой оси Y
temp[0] = Bernstein(py, patch.anchors[0]); // Вычислим новые точки Безье
temp[1] = Bernstein(py, patch.anchors[1]);
temp[2] = Bernstein(py, patch.anchors[2]);
temp[3] = Bernstein(py, patch.anchors[3]);
glBegin(GL_TRIANGLE_STRIP); // Начнем новую полоску треугольников
for (v=0;v<=divs;v++) {
px = ((float)v)/((float)divs); // Процент вдоль оси X
glTexCoord2f(pyold, px); // Применим старые координаты текстуры
glVertex3d(last[v].x, last[v].y, last[v].z); // Старая точка
last[v] = Bernstein(px, temp); // Генерируем новую точку
glTexCoord2f(py, px); // Применим новые координаты текстуры
glVertex3d(last[v].x, last[v].y, last[v].z); // Новая точка
}
glEnd(); // Конец полоски треугольников
}
glEndList(); // Конец списка
free(last); // Освободить старый массив вершин
return drawlist; // Вернуть список отображения
}
Далее зададим значения контрольных точек фрагмента, которые я подобрал, чтобы продемонстрировать эффект. Не стесняйтесь изменять эти значения и посмотреть, что же получится при этом.
void initBezier(void) {
mybezier.anchors[0][0] = makePoint(-0.75, -0.75, -0.50); // Вершины Безье
mybezier.anchors[0][1] = makePoint(-0.25, -0.75, 0.00);
mybezier.anchors[0][2] = makePoint( 0.25, -0.75, 0.00);
mybezier.anchors[0][3] = makePoint( 0.75, -0.75, -0.50);
mybezier.anchors[1][0] = makePoint(-0.75, -0.25, -0.75);
mybezier.anchors[1][1] = makePoint(-0.25, -0.25, 0.50);
mybezier.anchors[1][2] = makePoint( 0.25, -0.25, 0.50);
mybezier.anchors[1][3] = makePoint( 0.75, -0.25, -0.75);
mybezier.anchors[2][0] = makePoint(-0.75, 0.25, 0.00);
mybezier.anchors[2][1] = makePoint(-0.25, 0.25, -0.50);
mybezier.anchors[2][2] = makePoint( 0.25, 0.25, -0.50);
mybezier.anchors[2][3] = makePoint( 0.75, 0.25, 0.00);
mybezier.anchors[3][0] = makePoint(-0.75, 0.75, -0.50);
mybezier.anchors[3][1] = makePoint(-0.25, 0.75, -1.00);
mybezier.anchors[3][2] = makePoint( 0.25, 0.75, -1.00);
mybezier.anchors[3][3] = makePoint( 0.75, 0.75, -0.50);
mybezier.dlBPatch = NULL;
}
Это процедура загрузки одной картинки. Организовав цикл, Вы можете загрузить несколько картинок.
// Загрузить картинку и конвертировать ее в текстуру
BOOL LoadGLTexture(GLuint *texPntr, char* name)
{
BOOL success = FALSE;
AUX_RGBImageRec *TextureImage = NULL;
glGenTextures(1, texPntr); // Генерировать 1 текстуру
FILE* test=NULL;
TextureImage = NULL;
test = fopen(name, "r"); // Существует ли файл?
if (test != NULL) { // Если да
fclose(test); // Закрыть файл
TextureImage = auxDIBImageLoad(name); // И загрузить текстуру
}
if (TextureImage != NULL) { // Если загружена
success = TRUE;
// Обычная генерация текстура используя данные из картинки
glBindTexture(GL_TEXTURE_2D, *texPntr);
glTexImage2D(GL_TEXTURE_2D, 0, 3, TextureImage->sizeX, TextureImage->sizeY,
0, GL_RGB, GL_UNSIGNED_BYTE, TextureImage->data);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_LINEAR);
}
if (TextureImage->data)
free(TextureImage->data);
return success;
}
Инициализация фрагмента непосредственно здесь. Вы делаете это всякий раз, когда создаете фрагмент. Снова, это хорошее место использовать C++ (Безье класс).
int InitGL(GLvoid) // Настройки OpenGL
{
glEnable(GL_TEXTURE_2D); // Разрешить наложение текстуры
glShadeModel(GL_SMOOTH); // Разрешить сглаживание
glClearColor(0.05f, 0.05f, 0.05f, 0.5f); // Фон черный
glClearDepth(1.0f); // Настройки буфера глубины
glEnable(GL_DEPTH_TEST); // Разрешаем тест глубины
glDepthFunc(GL_LEQUAL); // Тип теста глубины
glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST); // Улучшенные вычисления перспективы
initBezier(); // Инициализация контрольной сетки Безье ( НОВОЕ )
LoadGLTexture(&(mybezier.texture), "./Data/NeHe.bmp"); // Загрузка текстуры ( НОВОЕ )
mybezier.dlBPatch = genBezier(mybezier, divs); // Создание фрагмента ( НОВОЕ )
return TRUE;
}
При отрисовке сцены, вначале отображаем список Безье. Затем (если контур включен) рисуются линии, соединяющие контрольные точки. Вы можете переключать этот режим при помощи ПРОБЕЛА.
int DrawGLScene(GLvoid) { // Здесь рисуем
int i, j;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // Очистка экрана и буфера глубины
glLoadIdentity(); // Сброс текущей матрицы вида модели
glTranslatef(0.0f,0.0f,-4.0f); // Сдвиг налево на 1.5 единицы и вглубь экрана на 6.0
glRotatef(-75.0f,1.0f,0.0f,0.0f);
glRotatef(rotz,0.0f,0.0f,1.0f); // Вращение по оси Z
glCallList(mybezier.dlBPatch);// Вызов списка Безье
// Это необходимо только в том случае, когда фрагмент изменился
if (showCPoints) { // Если отрисовка сетки включена
glDisable(GL_TEXTURE_2D);
glColor3f(1.0f,0.0f,0.0f);
for(i=0;i<4;i++) { // Нарисовать горизонтальную линию
glBegin(GL_LINE_STRIP);
for(j=0;j<4;j++)
glVertex3d(mybezier.anchors[i][j].x, mybezier.anchors[i][j].y, mybezier.anchors[i][j].z);
glEnd();
}
for(i=0;i<4;i++) { // Нарисовать вертикальную линию
glBegin(GL_LINE_STRIP);
for(j=0;j<4;j++)
glVertex3d(mybezier.anchors[j][i].x, mybezier.anchors[j][i].y, mybezier.anchors[j][i].z);
glEnd();
}
glColor3f(1.0f,1.0f,1.0f);
glEnable(GL_TEXTURE_2D);
}
return TRUE;
}
В этой функции код модифицирован, чтобы сделать его более совместимым. Эти изменения не имеют прямого отношения к кривым Безье, но при этом решается проблема с возвратом разрешения экрана после работы в полноэкранном режиме, которая имеется с некоторыми видеокартами (включая мою, дерьмовую старую ATI Rage PRO, и некоторыми другими). Я надеюсь, вы будете использовать эти модификации, так как они позволят вашим крутым программам работать должным образом. Делая эти модификации, проверьте, что Dmsaved определена и инициализирована, как это отмечено в функции CreateGLWindow().
GLvoid KillGLWindow(GLvoid) // Убить окно
{
if (fullscreen) // Мы в полноэкранном режиме?
{
if (!ChangeDisplaySettings(NULL,CDS_TEST)) {// Если это не работает ( НОВОЕ )
// Сделать это все равно (чтобы получить значения из системного реестра) (НОВОЕ)
ChangeDisplaySettings(NULL,CDS_RESET);
ChangeDisplaySettings(&DMsaved,CDS_RESET);// Изменить его на сохраненные настройки (НОВОЕ)
} else {
ChangeDisplaySettings(NULL,CDS_RESET); // Если это работает продолжаем (НОВОЕ)
}
ShowCursor(TRUE); // Показать курсор мыши
}
if (hRC) // Мы имеем контекст визуализации?
{
if (!wglMakeCurrent(NULL,NULL)) // Можно освободить контексты DC и RC?
{
MessageBox(NULL,"Release Of DC And RC Failed.","SHUTDOWN ERROR",
MB_OK | MB_ICONINFORMATION);
}
if (!wglDeleteContext(hRC)) // Действительно ли мы можем удалить RC?
{
MessageBox(NULL,"Release Rendering Context Failed.","SHUTDOWN ERROR",
MB_OK | MB_ICONINFORMATION);
}
hRC=NULL; // Установить RC в NULL
}
if (hDC && !ReleaseDC(hWnd,hDC)) // Действительно ли мы можем удалить DC
{
MessageBox(NULL,"Release Device Context Failed.","SHUTDOWN ERROR",
MB_OK | MB_ICONINFORMATION);
hDC=NULL; // Установить DC в NULL
}
if (hWnd && !DestroyWindow(hWnd)) // Действительно ли мы можем удалить окно?
{
MessageBox(NULL,"Could Not Release hWnd.","SHUTDOWN ERROR",
MB_OK | MB_ICONINFORMATION);
hWnd=NULL; // Set hWnd To NULL
}
// Действительно ли мы можем отменить регистрацию класса
if (!UnregisterClass("OpenGL",hInstance))
{
MessageBox(NULL,"Could Not Unregister Class.","SHUTDOWN ERROR",
MB_OK | MB_ICONINFORMATION);
hInstance=NULL; // Установить hInstance в NULL
}
}
В функции CreateGLWindow только добавлен вызов EnumDisplaySettings, чтобы сохранить параметры настройки дисплея.
BOOL CreateGLWindow(char* title, int width, int height, int bits, bool fullscreenflag)
{
. . . Код вырезан, чтобы уменьшить размер урока . . .
wc.lpszClassName = "OpenGL"; // Имя класса
// Сохранить текущие настройки дисплея (НОВОЕ)
EnumDisplaySettings(NULL, ENUM_CURRENT_SETTINGS, &DMsaved);
if (fullscreen) // Попробовать перейти в полноэкранный режим?
{
. . . Код вырезан, чтобы уменьшить размер урока . . .
return TRUE; // Успех
}
Здесь добавлен код для вращения фрагмента, уменьшения/улучшения разрешения, и переключения режима контура фрагмента.
int WINAPI WinMain( HINSTANCE hInstance, // Экземпляр
HINSTANCE hPrevInstance, // Предыдущий экземпляр
LPSTR lpCmdLine, // Параметры командной строки
int nCmdShow) // Состояние отображения окна
{
. . . Код вырезан, чтобы уменьшить размер урока . . .
SwapBuffers(hDC); // // Переключаем буферы (Двойная буферизация)
}
if (keys[VK_LEFT]) rotz -= 0.8f; // Вращение влево ( НОВОЕ )
if (keys[VK_RIGHT]) rotz += 0.8f; // Вращение вправо
if (keys[VK_UP]) { // Увеличить разрешение
divs++;
mybezier.dlBPatch = genBezier(mybezier, divs); // Обновить фрагмент
keys[VK_UP] = FALSE;
}
if (keys[VK_DOWN] && divs > 1) { // Уменьшить разрешения
divs--;
mybezier.dlBPatch = genBezier(mybezier, divs); // Обновить фрагмент
keys[VK_DOWN] = FALSE;
}
if (keys[VK_SPACE]) { // ПРОБЕЛ переключает showCPoints
showCPoints = !showCPoints;
keys[VK_SPACE] = FALSE;
}
if (keys[VK_F1]) // Если F1 нажата?
{
. . . Код вырезан, чтобы уменьшить размер урока . . .
return (msg.wParam); // Выходим из программы
}
Надеюсь, что этот урок осветил эту тему, и теперь вы полюбили кривые Безье, так же как и я. Если Вам понравился этот урок, я напишу еще урок о NURBS кривых. Пожалуйста, свяжитесь со мной по электронной почте и сообщите, что Вы думаете о моем уроке.
Об авторе: Дэвиду Никделу 18 лет и он учится в Bartow Senior High School. На данный момент он изучает кривые поверхности в 3D графике и игру на OpenGL под названием Blazing Sands. Его хобби — это программирование и футбол. Если все будет удачно, то в следующем году он поступит в Georgia Tech.
© David Nikdel
( ogapo@ithink.net )
© Jeff Molofee (NeHe)
11 сентября 2003 (c) Сергей Анисимов


