glBegin (GL_QUAD_STRIP); glVertex2iv (pl); glVertex2iv (p2); glVertex2iv (p4); glVertex2iv (p3); glVertex2iv (p5); glVertex2iv (p6); glVertex2iv (p8); glVertex2iv (p7); glEnd ( ) ; Четырехугольник задается для каждой пары вершин, идущей после первых двух вершин в списке, поэтому вершины нужно перечислять таким образом, чтобы каждый многоугольник имел правильный порядок вершин (против часовой стрелки). Для списка из N вершин получается ^ - 1 четырехугольников, при условии, что N > 4. Если N не кратно 4, то любые лишние координаты в списке учтены не будут. Эти закрашенные многоугольники и перечисленные вершины можно пронумеровать как п - 1, п = 2, …, п = у - 1. Тогда вершины четырехугольника п в таблице многоугольника будут перечислены в таком порядке (по номерам вершин): 2п - 1,
2п, 2п+2, 2п + 1. В данном примере N = 8, поэтому получается 3 четырехугольника. Таким образом, первый четырехугольник (п = 1) задается с таким порядком вершин (pl, р2, рЗ, р4). У второго четырехугольника (п = 2) порядок вершин - (р4, рЗ, рб, р5). А порядок вершин третьего четырехугольника (п = 3) - (р5, рб, р7, р8).
Во многих графических пакетах криволинейные поверхности изображаются с помощью аппроксимирующих плоских граней. Это объясняется тем, что уравнения плоскости линейны, а обработка линейных уравнений выполняется намного быстрее, чем обработка квадратных уравнений или уравнений других типов кривых. Поэтому OpenGL и другие пакеты предлагают примитивы многоугольников, которыми можно аппроксимировать криволинейные поверхности. Объекты моделируются с помощью сетки многоугольников, а информация о геометрических данных и данные о параметрах устанавливаются таким образом, чтобы можно было обрабатывать многоугольные грани. В пакете OpenGL для этой цели можно использовать такие примитивы, как полоса треугольников, веер треугольников и полоса четырехугольников. Высококачественные графические системы, способные изображать миллион или больше закрашенных многоугольников (как правило, треугольников) в секунду, включая приложения, связанные с наложением текстур на поверхности и специальных эффектов освещения, имеют встроенные аппаратные средства визуализации многоугольников.
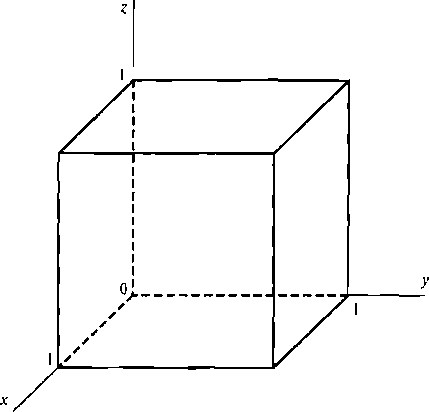
Рис. 3.58. Куб с единичной длиной ребра
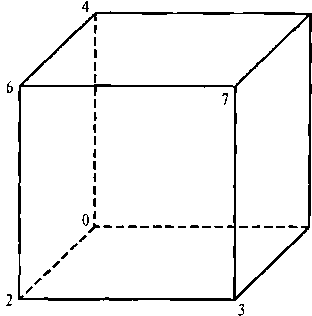
Рис. 3.59. Значения индексов для массива р1:, соответствующие координатам вершин куба, изображенного на рис. 3.58
Несмотря на то что корневая библиотека OpenGL принимает только выпуклые многоугольники, библиотека OpenGL Utility (GLU) предлагает функции, позволяющие работать с вогнутыми многоугольниками и другими невыпуклыми объектами с линейными границами. Существует набор стандартных процедур библиотеки GLU для мозаичного представления многоугольников, которые позволяют преобразовать такие фигуры в набор треугольников, треугольные сетки, веера треугольников и прямолинейные отрезки. Разложив эти объекты на составляющие, их можно обрабатывать с помощью основных функций OpenGL.
МАССИВЫ ВЕРШИН В OpenGL
Несмотря на то что до сих пор в приведенных примерах использовалось относительно немного координатных точек, реальное описание сцены, состоящей из нескольких объектов, может оказаться намного сложнее. Чтобы проиллюстрировать такую ситуацию, рассмотрим сначала описание одного очень простого объекта: единичного куба, изображенного на рис. 3.58, координаты которого (для простоты дальнейших рассуждений) заданы в виде целых чисел. Прямой метод определения координат вершин заключается в использовании массива с двумя индексами, такого как
