Чтобы определить направление границы в точке пересечения, можно представить стороны объекта (или отрезки, образующие границу) в виде векторов, а также задать направление опорной линии. После этого для каждой стороны, с которой пересекается опорная линия, вычисляется векторное произведение вектора и, направленного по опорной прямой от точки Р к удаленной точке, и вектора стороны объекта Е. Предположим, что дан двухмерный объект на плоскости ху. Тогда все векторные произведения будут направлены либо по +г, либо по -2. Если компонент 2 векторного произведения и х Е для определенной точки пересечения положителен, то отрезок пересекает прямую справа налево, и к количеству витков прибавляется 1. В противном случае отрезок пересекает прямую слева направо, и от количества витков отнимается 1.
Возможно, еще более простым способом определения направления в точке пересечения с границей является использование не векторного, а скалярного произведения векторов. Для этого нужно задать вектор, перпендикулярный вектору и и направленный справа налево, если смотреть вдоль опорной прямой из точки Р в направлении вектора и. Если компоненты вектора и обозначить как (их, иу), компоненты вектора, перпендикулярного к вектору и, будут равны (-иу, их) (приложение А). Если теперь скалярное произведение этого перпендикулярного вектора и вектора, проложенного по границе, положительное, то направление пересечения - справа налево, и к количеству витков нужно прибавить единицу. В противном случае граница пересекает опорную линию слева направо, и от количества витков отнимается единица.
Правило ненулевого количества витков часто относит к внутренним некоторые области, которые при применении правила четного-нечетного считаются внешними, а в некоторых приложениях этот метод может быть еще более непредсказуемым. В общем случае, плоские фигуры могут состоять из множества не связанных между собой элементов, и в таком случае для определения внутренних и внешних областей можно использовать направление, которое задается для каждого набора не связанных между собой границ. К числу таких фигур относятся символы (буквы алфавита или знаки пунктуации), вложенные многоугольники, концентрические круги или эллипсы. Для кривых линий правило четного-нечетного применяется в форме подсчета числа точек пересечения с кривой. Аналогично для правила ненулевого количества витков необходимо найти векторы, направленные по касательной к кривой в точках ее пересечения с опорной прямой, проходящей через точку Р.

Рис. 3.47. Закрашенная область, определенная как сегмент, для которого число витков положительно. Она представляет собой объединение двух областей, граница каждой из которых обходится против часовой стрелки
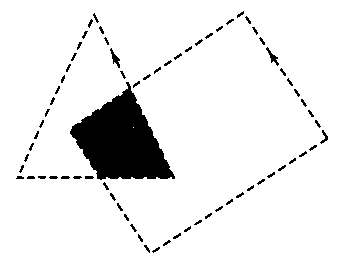
Рис. 3.48. Закрашенная область, определенная как сегмент, для которого число витков больше 1. Она представляет собой область наложения двух фигур, граница каждой из которых направлена против часовой стрелки Некоторые разновидности правила ненулевого количества витков позволяют несколько иначе определять внутренние области. Например, точку можно считать внутренней, если количество витков для нее положительно или если оно отрицательно. Кроме того, можно воспользоваться любым другим правилом и создать ряд закрашенных фигур. Иногда закрашенная область задается в виде комбинации двух областей с помощью логических (булевых) операций при использовании одной из разновидностей стандартного алгоритма ненулевого числа витков. Согласно этой схеме сначала для каждой из двух областей находятся простые, непересекающиеся границы. Тогда, если считать, что каждая граница обходится против часовой стрелки, объединение двух областей будет состоять из точек с положительным количеством витков (рис. 3.47). Аналогично область пересечения двух фигур, границы которых обходятся против часовой стрелки, будет содержать только те точки, количество витков которых превышает 1, как показано на рис. 3.48. Чтобы задать закрашенную область, которая представляет собой разность двух областей, скажем, А - В, можно обвести область А границей, направленной против часовой стрелки, а область В - границей, направленной по часовой стрелке. Тогда область разности (рис. 3.49) будет представлять собой набор всех точек, для которых число витков положительное.
