МЕТОДЫ ДЕЛЕНИЯ ПРОСТРАНСТВА
Другой путь сокращения расчетов - использовать процедуры деления пространства. Всю сцену можно замкнуть в куб, затем последовательно делить его, пока каждая подобласть (ячейка) не будет содержать не более, чем заданное минимальное число поверхностей. Например, можно потребовать, чтобы каждая ячейка содержала не более одной поверхности. Если доступны возможности параллельной и векторной обработки, максимальное число поверхностей на ячейку можно определить по размеру векторного регистра и числу процессов. Деление пространства куба можно представить в октодереве или ВБР-дереве. Кроме того, можно выполнить равномерное
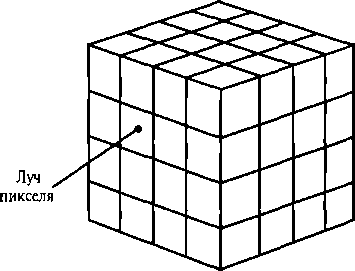
Рис. 10.65. Пересечение луча с кубом, вмещающим все объекты на сцене
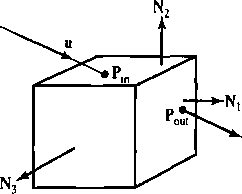
Рис. 10.66. Прохождение луча через подобласть (ячейку) куба, вмещающего сцену деление, на каждом шаге разбивая куб на восемь равных октантов, или адаптивное деление, разбивая только те области куба, которые содержат объекты.
Затем через отдельные ячейки куба строится путь лучей, причем проверки на пересечение выполняются только в ячейках, содержащих поверхности. Первая пересеченная лучом поверхность является видимой поверхностью для этого луча. Стоит отметить, что существует определенная связь между размером ячейки и числом поверхностей на ячейку. Если снижать максимальное число разрешенных поверхностей на ячейку, сокращается объем вычислений, необходимых для проверок пересечения поверхности, но при этом также сокращается размер ячейки, так что для определения пути луча через ячейки требуется больше вычислений.
На рис. 10.65 иллюстрируется пересечение луча пикселя с передней гранью куба, окружающего сцену. Точка пересечения на передней грани куба определяет исходную ячейку, которую пройдет луч. Чтобы провести луч через ячейки куба, можно определить координаты точек входа и выхода (рис. 10.66). В каждой непустой ячейке проверяется возможность пересечения луча с поверхностью. Описанная обработка продолжается, пока луч не пересечет поверхность объекта или не выйдет из граничного куба.

Рис. 10.69. Визуализация приведенной сцены с построением хода лучей требует 24 секунды на параллельном компьютере KSR1 (Kendall Square Research) с 32 процессорами. Роденовский Мыслитель смоделирован 3 036 примитивами. Для получения глобальных эффектов освещения по 1 675 776 обработанным лучам использовались два источника света и один первичный луч на пиксель (перепечатано с разрешения М. Дж. Ки-тиса (М. J. Keates) и Р. Дж. Хабболъда (R. J. Hubbold), факультет информации, Манчестерский университет, Великобритания)
Сцена на рис. 10.68 была получена построением хода лучей с использованием методов деления пространства. Без деления пространства расчет занимал в 10 раз больше времени. Если удалить со сцены многоугольники, выигрыш от использования деления пространства еще больше - для сцены, содержащей 2 048 сфер и ни одного многоугольника, тот же алгоритм выполняется в 46 раза быстрее стандартного алгоритма построения хода лучей.
На рис. 10.69 иллюстрируется другая сцена, для создания которой применялось построение хода лучей с использованием деления пространства и методы параллельной обработки. Данное изображение скульптуры Родена Мыслитель визуализировалось за 24 секунды при использовании более 1,5 миллионов лучей.
