Методика визуализации также используется для облегчения понимания и анализа сложных процессов и математических функций. Цветной график кривых математических функций показан на рис. 1.24, а изображение функции в виде поверхности представлено на рис. 1.25. Фрактальные процедуры с использованием кватернионов дают объект, изображенный на рис. 1.26, а на рис. 1.27 показаны топологические структуры. Ученые также разрабатывают методы визуализации общих классов данных. На рис. 1.28 показан общий метод графического изображения и моделирования данных, расположенных на сферической поверхности.
Некоторые из множества других областей применения визуализации показаны на рис. 1.29-1.42. На этих рисунках изображены: воздушные потоки на поверхности космического корабля, численное моделирование грозы, развитие трещин в металлах, цветовое кодирование плотности потока над аэродинамической поверхностью (крылом), ряд поперечных разрезов набора данных, моделирование белков, интерактивная схема молекулярных структур в виртуальной реальности, модель дна океана, моделирование кувейтских нефтяных пожаров, исследование загрязнений атмосферы, динамика роста кукурузы, реконструкция развалин каньона Чако в Аризоне и график, отображающий статистику автомобильных аварий.
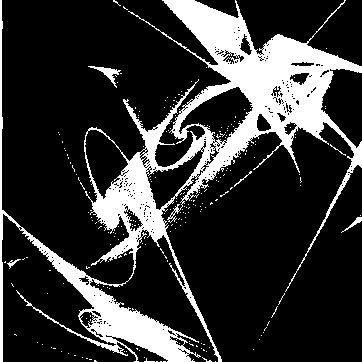
Рис. 1.24. Кривые математических функций, построенные с помощью различных цветовых комбинаций (перепечатано с разрешения Мелвина Прюитта (Melvin L. Prueitt), Национальная лаборатория Лос-Аламоса)

Рис. 1.25. Для представления этой трехмерной функции в виде закрашенной поверхности применялось моделирование освещения и закрашивание поверхностей (перепечатано с разрешения Wolfram Research, Inc., создателя программы Mathematical

Рис. 1.26. Четырехмерный объект, спроектированный сначала в трехмерное пространство, а затем - на двухмерный экран монитора и прошедший цветовое кодирование. Этот объект был создан с помощью кватернионов и процедуры фрактального возведения в квадрат (перепечатано с разрешения Джона Харта (John C. Hart), факультет кибернетики Иллинойского университета в Урбана-Шампейн)
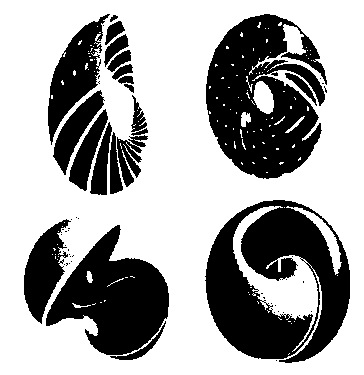
Рис. 1.27. Четыре изображения из интерактивного исследования в реальном времени с помощью компьютерной анимации минимальных поверхностей (“улиток”) в трехмерной сфере, спроектированных в трехмерное евклидово пространство (перепечатано с разрешения Джорджа Франсиса (George Francis), факультет математики, и Национального центра суперкомпьютерных приложений Иллинойско-го университета в Урбана-Шампейн. © 1993)

Рис. 1.28. Метод отображения графической информации и моделирования данных, расположенных на поверхности сферы (перепечатано с разрешения Грега Нельсона (Greg Nelson), факультет кибернетики Национального университета Аризоны)

Рис. 1.29. Визуализация поверхностей потоков, сопровождающих космический корабль, разработанная Джеффом Халткви-стом (Jeff Hultquist) и Эриком Рейблом (Eric Raible) для испытаний НАТО (перепечатано с разрешения Сэма Юзлтона (Sam Usel-ton), Исследовательский центр НАТО)

Рис. 1.30. Численная модель воздушного потока во время грозы (перепечатано с разрешения Боба Вильгелъмсона (Bob Wilhelmson). факультет атмосферных наук, и Национального центра супер-компьютерных приложений, Ил-линойский университет в Урбана-Шампейн)
