ФУНКЦИИ МНОГОГРАННИКОВ OpenGL
Многоугольные поверхности в программе OpenGL можно задать двумя способами. - помощью многоугольных примитивов, рассмотренных в разделе 3.16, можно сгенерировать множество форм многоугольников и сеток поверхностей. Кроме того, можно использовать функции GLUT вывода на экран пяти правильных многогранников.
ФУНКЦИИ OpenGL ЗАПОЛНЕНИЯ ОБЛА-ТИ МНОГОУГОЛЬНИКА
Чтобы ввести набор многоугольных участков для фрагмента поверхности объекта или полное описание многогранника, можно использовать константы (примитивы) OpenGL GL_POLYGON, GL_TRIANGLES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_QUADS и GL_QUAD_STRIP. Таким образом можно, например, представить боковую поверхность цилиндра в виде мозаичной структуры с помощью четырехугольной полоски. Аналогично все стороны параллелограмма можно описать набором многоугольников, а все грани треугольной пирамиды задать с помощью набора связанных треугольных поверхностей.
ФУНКЦИИ GLUT ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
В процедурах библиотеки GLLTT предопределены некоторые стандартные формы (пять правильных многогранников). Отличительной особенностью данных многогранников, также называемых телами Платона, является то, что все грани любого правильного многогранника - идентичные правильные многоугольники. -ледовательно, все стороны правильного многогранника равны, все плоские углы при вершинах равны, и все углы между гранями также равны. Многогранники названы согласно числу граней: правильный тетраэдр (или треугольная пирамида, 4 грани), правильный гексаэдр (или куб, 6 граней), правильный октаэдр (8 граней), правильный додекаэдр (12 граней) и правильный икосаэдр (20 граней).
Библиотека GLUT предлагает 10 функций генерации названных тел: пять функций дают каркасные объекты, пять отображают грани многогранников как затененные закрашенные области. Характеристики закрашиваемой области определяются свойствами материала и условиями освещения, заданными для сцены. Все правильные многогранники описываются в модельных координатах, так что все они центрированы в начале внешней системы координат.
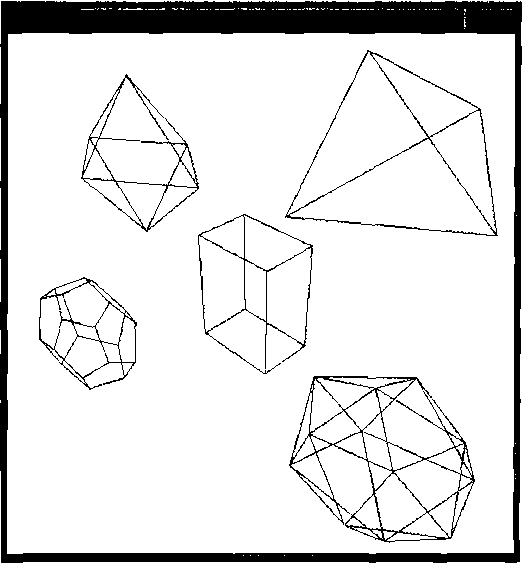
Рис. 8.1. Перспективная проекция пяти многогранников GLUT, масштабированных и размещенных в окне на экране дисплея с помощью процедуры displayWirePoly-hedra
ПРИМЕР ПРОГРАММЫ GLUT ПО-ТРОЕНИЯ МНОГОГРАННИКОВ
В приведенной ниже программе с помощью функций GLUT вывода на экран тел Платона генерируются преобразованные каркасные перспективные изображения данных многогранников. Все пять тел размещаются в пределах одного окна (рис. 8.1).
♦include <GL/glut.h>
GLsizei winWidth = 500, winHeight = 500;
/* Исходный размер окна. */ void init (void)
{
glClearColor (1.0, 1.0, 1.0, 0.0); // Белое окно на экране.
}
void displayWirePolyhedra (void)
{
glClear (GL_COLOR_BUFFER_BIT); // Очистить окно. glColor3f (0.0, 0.0, 1.0); // -делать цвет линий синим.
/* Задать преобразование точки наблюдения. */ gluLookAt (5.0, 5.0, 5.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);
/* Масштабировать куб и отобразить его в виде
* каркасного параллелепипеда.
