*/
if (inside (р, winEdge, wMin, wMax)) if (winEdge < Top)
clipPoint (p, winEdge + 1, wMin, wMax, pOut, cnt, first, s); else {
pOut[*cnt] = p; (*cnt)++;
}
void closeClip (wcPt2D wMin, wcPt2D wMax, wcPt2D * pOut,
GLint * cnt, wcPt2D * first [ ], wcPt2D * s)
{
wcPt2D pt;
Boundary winEdge;
for (winEdge = Left; winEdge <= Top; winEdge++) { if (cross (sfwinEdge], *first[winEdge], winEdge, wMin, wMax)) { pt = intersect (s[winEdge],
*first[winEdge], winEdge, wMin, wMax); if (winEdge < Top)
clipPoint (pt, winEdge + 1, wMin, wMax, pOut, cnt,
first, s);
else {
pOut[*cnt] = pt; (*cnt)++;
}
}
}
}
GLint polygonClipSuthHodg (wcPt2D wMin, wcPt2D wMax, GLint n,
wcPt2D * pin, wcPt2D * pOut)
{
/* Параметр "first" содержит указатель на первую точку,
* обработанную для границы; "s" содержит последнюю
* точку, обработанную с данной границей.
*/
wcPt2D * first[nClip] = 0, 0, 0, 0 , s[nClip];
GLint k, cnt = 0;
for (k = 0; k < n; k++)
clipPoint (pln[k], Left, wMin, wMax, pOut, Sent, first, s); closeClip (wMin, wMax, pOut, Sent, first, s); return (cnt);
}
Если с помощью алгоритма Сазерленда-Ходгмана обрабатывается вогнутый многоугольник, на экран могут выводиться посторонние линии. Пример такой ситуации приведен на рис. 6.28. Это происходит, когда обработанный многоугольник должен иметь несколько отдельных участков, но, поскольку существует только один выходной список вершин, последняя вершина списка всегда соединяется с первой.
Для корректного отсечения вогнутых многоугольников можно предпринять некоторые действия. Во-первых, вогнутый многоугольник можно расщепить на несколько выпуклых (раздел 3.15) и обработать каждый полученный многоугольник отдельно с использованием алгоритма Сазерленда-Ходгмана. Во-вторых, можно модифицировать этот алгоритм, чтобы конечный набор вершин проверялся на наличие нескольких точек пересечения вдоль границы отсекающего окна. Если обнаружено более двух
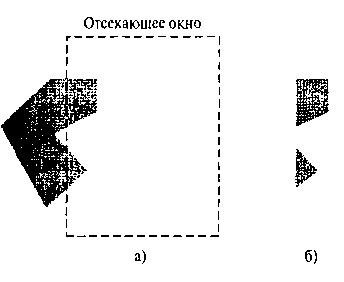
Рис. 6.28. Отсечение вогнутого многоугольника (панель а) с использованием алгоритма Сазерленда-Ходгмана дает две связанные области (панель б)
вершин вдоль границы отсечения, данный список можно разделить на несколько списков, верно идентифицирующих участки обрезанной закрашенной области. Это может требовать досконального анализа, выявляющего, точки вдоль границы отсечения образуют пары или являются отдельными вершинами конечного многоугольника. В-третьих, можно использовать более общую процедуру отсечения многоугольников, разработанную для корректной обработки вогнутых многоугольников.
АЛГОРИТМ ОТСЕЧЕНИЯ МНОГОУГОЛЬНИКОВ УЭЙЛЕРА-АЗЕРТОНА
Данный алгоритм - это общий подход к отсечению многоугольников, который можно использовать для отсечения закрашенной области выпуклого или вогнутого многоугольника. Более того, этот метод разрабатывался как средство идентификации видимых поверхностей трехмерной сцены. Следовательно, его также можно использовать для отсечения любой многоугольной области с помощью окна произвольной многоугольной формы.
