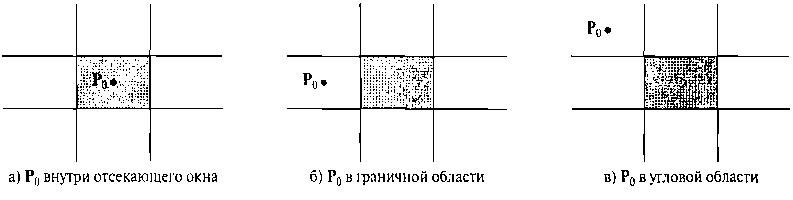
Рис. 6.16. Три возможных положения конечной точки линии Ро в алгоритме НЛН но вычислять точки пересечения вдоль траектории прямой, даже если сам отрезок полностью находится за отсекающим окном. Наконец, каждый этап вычисления точки пересечения по Кохену-Сазерленду требует деления и умножения. В завершение отметим, что алгоритм Лианга-Барски можно расширить на отсечение трехмерных линий (глава 7).

ОТСЕЧЕНИЕ ЛИНИИ НИКОЛЛА-ЛИ-НИКОЛЛА

В алгоритме Николла-Ли-Николла (Nicholl-Lee-Nicholl - NLN, НЛН) создается больше областей вокруг окна отсечения, и за счет этого не нужно несколько раз проводить расчет точек пересечения линии с окном. В методе Коэна-Сазерленда, например, можно вначале вычислить несколько точек пересечения вдоль прямой, содержащей отрезок, перед тем, как будет найдена точка пересечения с собственно отсекающим прямоугольником, или пока линия не будет целиком отброшена. В алгоритме НЛН подобных дополнительных расчетов нет, для чего перед вычислением точки пересечения выполняется больше проверок областей. По сравнению с алгоритмами Коэна-Сазерленда и Лианга-Барски алгоритм НЛН имеет меньше операций сравнения и деления. За эти преимущества нужно платить тем, что алгоритм НЛН применим только к двухмерному отсечению, тогда как два других легко расширяются на трехмерные сцены.

Изначальную проверку, выполняемую, чтобы определить, находится отрезок целиком внутри или целиком снаружи окна, можно провести с использованием кодов областей, как в предыдущих двух алгоритмах. Если тривиальное принятие или отклонение отрезка невозможно, алгоритм НЛН вводит дополнительные области отсечения.

Для отрезка с концами Ро и P_end вначале определяется положение точки Ро в восьми возможных областях относительно отсекающего окна. Из показанных на рис. 6.16 областей нужно рассмотреть только три. Если точка Ро лежит в одной из шести остальных областей, ее можно переместить в одну из трех областей, показанных на рис. 6.16, используя преобразование симметрии. Например, область непосредственно над отсекающим окном можно преобразовать в область слева от окна, используя отражение относительно линии у - -х, или же можно использовать поворот на 90° против часовой стрелки.

ОТСЕЧЕНИЕ МНОГОУГОЛЬНОЙ ЗАКРАШЕННОЙ ОБЛАСТИ

Графические пакеты обычно поддерживают только закрашенные области, являющиеся многоугольниками, причем часто - только выпуклыми. Чтобы обрезать многоугольную закрашенную область, нельзя прямо применить метод отсечения линии к отдельным сторонам многоугольника, поскольку данный подход в общем случае не даст замкнутой ломаной линии. Вместо этого алгоритм отсечения линии часто дает непересекающийся набор линий, причем без указания полной информации о том, как можно сформировать замкнутую границу вокруг извлеченной закрашенной области. На рис. 6.21 иллюстрируется возможный выход процедуры отсечения линий, примененной к сторонам многоугольной закрашенной области. Итак, все, что требуется, - процедура, которая выдаст одну или несколько замкнутых ломаных линий-границ извлеченной закрашенной области, чтобы многоугольники можно было преобразовать в стандарт развертки и заполнить внутренние части заданным цветом или узором, как показано на рис. 6.22.

⇐ вернуться назад | | далее ⇒