МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ И ОДНОРОДНЫЕ КООРДИНАТЫ
Во многих графических приложениях реализованы последовательности геометрических преобразований. В анимации может потребоваться транслировать и поворачивать объект на последовательность кадров. В приложениях разработки и построения изображений трансляция, повороты и масштабирование выполняются для того, чтобы правильно разместить компоненты изображения в нужных местах. Кроме того, преобразование наблюдения включает в себя последовательность трансляций и поворотов, необходимых, чтобы перейти от исходной спецификации сцены к изображению на устройстве вывода. Ниже показывается, как матричные представления, рассмотренные в предыдущих разделах, можно переформулировать так, чтобы последовательности преобразования обрабатывались эффективно.
Чтобы с помощью этих уравнений получить последовательность преобразований (например, масштабирование с последующим поворотом и трансляцией), можно рассчитать преобразованные координаты поэтапно. Вначале точки масштабируются, затем поворачиваются и транслируются. Однако гораздо эффективнее вначале объединить преобразования, чтобы координаты конечных точек получались непосредственно из координат исходных, без расчета координат промежуточных точек. Для этого можно переформулировать уравнение (5.15) и исключить из него операцию матричного сложения.
ПРИМЕР ПРОГРАММИРОВАНИЯ ДВУХМЕРНОЙ СЛОЖНОЙ МАТРИЦЫ
В качестве примера реализации последовательности геометрических преобразований ниже приводится программа OpenGL. Изначально сложная матрица compMatrix активизируется как единичная матрица. В этом примере для построения сложной матрицы преобразования используется порядок свертки слева направо, и процедуры преобразования вызываются в порядке их выполнения. При вызове процедуры каждого базового преобразования (масштабирование, поворот и трансляция) матрица этого преобразования определяется и множится слева на сложную матрицу. После того как все преобразования будут заданы, сложное преобразование применяется к треугольнику. В результате треугольник вначале масштабируется относительно центра масс (приложение А), затем поворачивается вокруг него и, наконец, транслируется. На рис. 5.15 показаны исходное и конечное положение треугольника, преобразованного указанной последовательностью операций. Для вывода исходного и конечного положения треугольника на экран используются процедуры OpenGL.
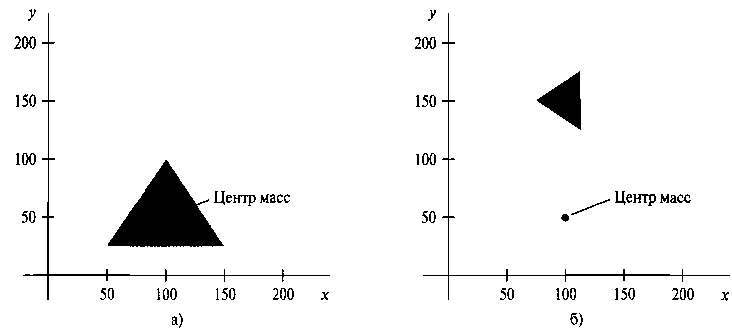
Рис. 5.15. Треугольник (панель о) преобразовывается в положение (панель б) с использованием сложной матрицы, рассчитанной в процедуре ^апз!:огт\/егЪз20
♦include <GL/glut.h>
♦include <stdlib.h>
♦include <math.h>
/* Задается исходный размер окна на экране дисплея. */ GLsizei winWidth = 600, winHeight = 600;
/* Задается диапазон изменения внешних координат. */ GLfloat xwcMin * 0.0, xwcMax = 225.0;
GLfloat ywcMin = 0.0, ywcMax - 225.0; class wcPt2D { public:
GLfloat x, y;
} ;
typedef GLfloat Matrix3x3 [3][3];
Matrix3x3 matComposite; const GLdouble pi = 3.14159;
void init (void)
<
/* Устанавливается цвет окна - белый. */ glClearColor (1.0, 1.0, 1.0, 0.0);
