Ради получения этих преимуществ сверхдискретизации прямой с конечной шириной необходимо идти на компромисс, который заключается в том, что для определения внутренних подпикселей необходимо больше вычислений, чем просто для определения того, какие подпиксели попадают на траекторию прямой. К тому же, необходимо учитывать положение границ прямой относительно ее траектории. Это положение зависит от угла наклона прямой. Для прямой, расположенной под углом 45°, траектория прямой проходит по центру многоугольника; но при работе с горизонтальной или вертикальной прямой хотелось бы, чтобы одной из границ многоугольника была сама прямая. Приведем такой пример: горизонтальную линию, проходящую через точку с координатами сетки (10, 20), можно было бы представить как многоугольник, ограниченный горизонтальными линиями сетки у = 20 и у = 21. Аналогично многоугольник, представляющий собой вертикальную линию, которая проходит через точку (10, 20), может иметь вертикальные границы, совпадающие с линиями сетки х = 10 и х = 11. Для прямых, тангенс угла наклона которых \т\ < 1, математическая траектория прямой располагается пропорционально ближе к нижней границе многоугольника; а для прямых, тангенс угла наклона которых \т\ > 1, траектория прямой проходит ближе к верхней границе многоугольника.
МАСКИ УДЕЛЬНОГО ВЕСА ПОДПИКСЕЛЕЙ
Алгоритмы сверхдискретизации часто реализуются путем учета с большими весовыми коэффициентами тех подпикселей, которые находятся в центре пикселя, поскольку можно ожидать, что эти подпиксели будут более значимыми при определении общей интенсивности пикселя. При делении пикселя на сетку размером 3 на 3, которое мы рассматривали до сих пор, можно пользоваться такой схемой распределения удельного веса, которая показана на рис. 4.49. Здесь центральный подпиксель идет с весовым коэффициентом, который в четыре раза больше, чем угловые, и в два раза больше, чем остальные подпиксели. Затем при усреднении интенсивностей, рассчитанных для каждого из девяти подпикселей, интенсивность центрального подпикселя умножается на весовой коэффициент верхний, нижний и боковые подпиксели умножаются на коэффициент а угловые подпиксели умножаются на коэффициент Массив значений, описывающих относительный вклад каждого подпикселя, обычно называют маской удельного веса. Аналогичные маски можно задавать и для больших сеток
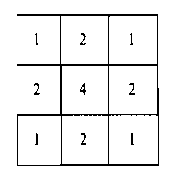
Рис. 4.49. Удельный вес подпикселей сетки размером 3 на 3
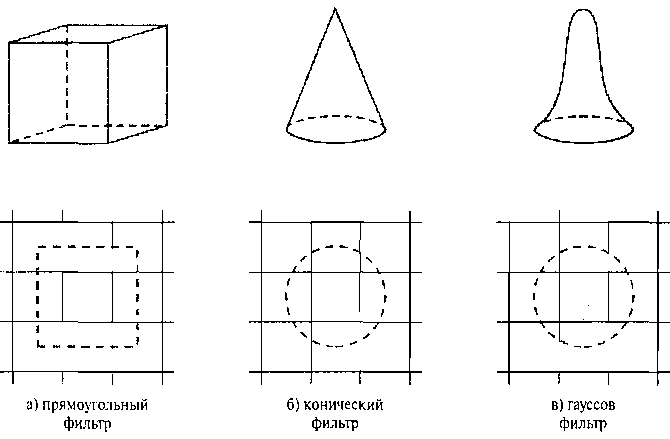
Рис. 4.50. Характерные фильтрующие функции, которые используются для устранения контурных неровностей прямых линий. Объем каждого фильтра нормирован на 1, а значение высоты дает относительный удельный вес каждого подпикселя подпикселей. Кроме того, часто эти маски дополняют таким образом, чтобы в них учитывались вклады подпикселей, принадлежащих к соседним пикселям; чтобы можно было усреднять интенсивности примыкающих друг к другу пикселей и получать более равномерное распределение интенсивности между пикселями.
ДИСКРЕТИЗАЦИЯ ПРЯМОЛИНЕЙНЫХ ОТРЕЗКОВ ПО ПЛОЩАДИ
Дискретизация прямолинейных отрезков по площади выполняется путем присвоения пикселям значений интенсивности, пропорциональных площади перекрывания пикселя прямой линией конечной ширины. Прямую линию можно рассматривать как прямоугольник, а отрезок прямой, лежащий между двумя соседними вертикальными (или горизонтальными) линиями сетки экрана, - как трапецию. Чтобы вычислить площади перекрывания пикселей, следует определить, какая часть трапеции перекрывается каждым пикселем в этом столбце (или строке). На рис. 4.48 пиксель с координатами сетки экрана (10, 20) приблизительно на 90 % перекрывается площадью прямой, поэтому его интенсивность будет иметь значение, равное 90 % от максимальной интенсивности. Аналогично пикселю с координатами (10, 21) будет присвоено значение, равное 15 % от максимальной интенсивности. Метод оценки площади перекрывания пикселя показан на рис. 4.48. Общее количество подпикселей, попадающих в пределы прямой линии, приблизительно равно площади перекрывания, а уточнить это значение можно, используя более мелкую сетку подпикселей.
