□ Качество растровых изображений ухудшается при сильном масштабировании.
Последний пункт нужно пояснить на примере. Предположим, что мы имеем небольшое растровое изображение, и у нас возникло желание его увеличить. Откроем его в программе графического редактора, выполним команду увеличения и… Получим результат, показанный на рис. 1.2.
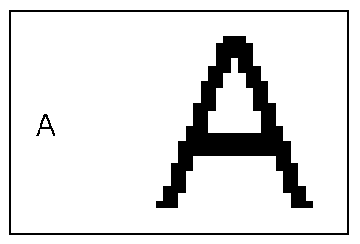
Рис. 1.2. Результат увеличения растрового изображения (слева - изначальное изображение, справа - увеличенное)
Слева на рис. 1.2 показано исходное изображение, справа - результат его увеличения. Видно, что каждый пиксел исходного изображения увеличился до размеров огромного "кирпича", в результате чего правое изображение сильно исказилось.
Как можно преодолеть этот недостаток?
Во-первых, по мере возможности не следует менять размеры растровых изображений. Лучше всего создавать их именно такого размера, какой нужен. В крайнем случае их можно уменьшить или совсем немного увеличить, чтобы точечная структура была незаметна.
Во-вторых, рекомендуется использовать достаточно мощные графические пакеты, например, последние версии Adobe Photoshop, для масштабирования растровой графики. Реализованные в них алгоритмы позволяют менять размеры изображений практически без потерь качества. Поставляемый в составе Microsoft Windows простейший графический редактор Paint этого не может.
Что касается первого недостатка растровой графики - прямой зависимости размера графического файла от геометрических размеров изображения - то он также практически преодолен. Дело в том, что подавляющее большинство графических форматов предоставляют возможность сжатия массива пикселов, в результате которого размер графического файла сильно уменьшается. Правда, такой подход чреват ростом затрат процессорного времени на распаковку изображения и риском потери данных при использовании слишком сильного сжатия.
Вот и все о растровой графике. Предоставим слово конкурирующей стороне.
Векторная графика
Рассказ о векторной графике мы начнем с небольшого допущения. Предположим, что любое, даже очень сложное графическое изображение можно разбить на простейшие элементы: прямые и кривые линии, эллипсы, прямоугольники и т. п. Эти простейшие элементы, называемые примитивами, описываются с помощью определенных формул. В результате мы получим набор параметров для этих формул, используя которые, можно точно воссоздать исходный набор примитивов, а значит и исходное изображение. Так вот, графика, состоящая из примитивов, и называется векторной графикой.
В качестве примера возьмем все ту же литеру А в векторном представлении. Если внимательно присмотреться к ней (рис. 1.3), можно увидеть, что она состоит из трех примитивов - прямых линий. (На рис. 1.3 они немнсго отделены друг от друга для лучшей наглядности.)

Рис. 1.3. Векторное представление литеры А
Но, спросите вы, как же компьютер выводит векторные изображения на экран? Ведь экран компьютера - это растр, и компьютер должен сначала преобразовать изображение в набор пикселов, т. е. растрироватъ его? Вы правы. Да, компьютер растрирует векторную графику, для чего дополнительно тратятся его системные ресурсы. Затраты системных ресурсов на растеризацию - один из главнейших недостатков векторной графики, но неоспоримые достоинства с лихвой его окупают.
