Troubleshooting TransformationsIt's pretty easy to get a camera pointed in the right direction, but in computer graphics, you have to specify position and direction with coordinates and angles. As we can attest, it's all too easy to achieve the well-known black-screen effect. Although any number of things can go wrong, often you get this effect - which results in absolutely nothing being drawn in the window you open on the screen - from incorrectly aiming the "camera" and taking a picture with the model behind you. A similar problem arises if you don't choose a field of view that's wide enough to view your objects but narrow enough so they appear reasonably large. If you find yourself exerting great programming effort only to create a black window, try these diagnostic steps.
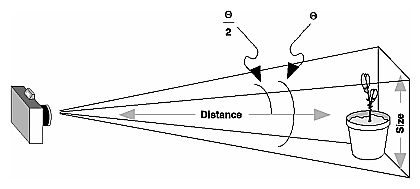
Even after you've aimed the camera in the correct direction and you can see your objects, they might appear too small or too large. If you're using gluPerspective(), you might need to alter the angle defining the field of view by changing the value of the first parameter for this command. You can use trigonometry to calculate the desired field of view given the size of the object and its distance from the viewpoint: The tangent of half the desired angle is half the size of the object divided by the distance to the object (see Figure 3-19). Thus, you can use an arctangent routine to compute half the desired angle. Example 3-3 assumes such a routine, atan2(), which calculates the arctangent given the length of the opposite and adjacent sides of a right triangle. This result then needs to be converted from radians to degrees.
Figure 3-19 : Using Trigonometry to Calculate the Field of View Example 3-3 : Calculating Field of View #define PI 3.1415926535 double calculateAngle(double size, double distance) {
double radtheta, degtheta; radtheta = 2.0 * atan2 (size/2.0, distance); degtheta = (180.0 * radtheta) / PI; return (degtheta); } Of course, typically you don't know the exact size of an object, and the distance can only be determined between the viewpoint and a single point in your scene. To obtain a fairly good approximate value, find the bounding box for your scene by determining the maximum and minimum x, y, and z coordinates of all the objects in your scene. Then calculate the radius of a bounding sphere for that box, and use the center of the sphere to determine the distance and the radius to determine the size. For example, suppose all the coordinates in your object satisfy the equations -1 ≤ x ≤ 3, 5 ≤ y ≤ 7, and -5 ≤ z ≤ 5. Then the center of the bounding box is (1, 6, 0), and the radius of a bounding sphere is the distance from the center of the box to any corner - say (3, 7, 5) - or
If the viewpoint is at (8, 9, 10), the distance between it and the center is
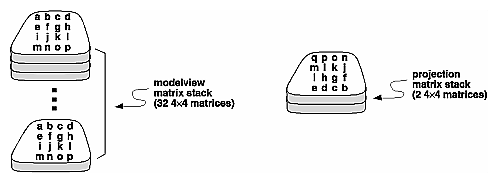
The tangent of the half angle is 5.477 divided by 12.570, which equals 0.4357, so the half angle is 23.54 degrees. Remember that the field-of-view angle affects the optimal position for the viewpoint, if you're trying to achieve a realistic image. For example, if your calculations indicate that you need a 179-degree field of view, the viewpoint must be a fraction of an inch from the screen to achieve realism. If your calculated field of view is too large, you might need to move the viewpoint farther away from the object. Manipulating the Matrix StacksThe modelview and projection matrices you've been creating, loading, and multiplying have only been the visible tips of their respective icebergs. Each of these matrices is actually the topmost member of a stack of matrices (see Figure 3-20).
Figure 3-20 : Modelview and Projection Matrix Stacks A stack of matrices is useful for constructing hierarchical models, in which complicated objects are constructed from simpler ones. For example, suppose you're drawing an automobile that has four wheels, each of which is attached to the car with five bolts. You have a single routine to draw a wheel and another to draw a bolt, since all the wheels and all the bolts look the same. These routines draw a wheel or a bolt in some convenient position and orientation, say centered at the origin with its axis coincident with the z axis. When you draw the car, including the wheels and bolts, you want to call the wheel-drawing routine four times with different transformations in effect each time to position the wheels correctly. As you draw each wheel, you want to draw the bolts five times, each time translated appropriately relative to the wheel. Suppose for a minute that all you have to do is draw the car body and the wheels. The English description of what you want to do might be something like this:
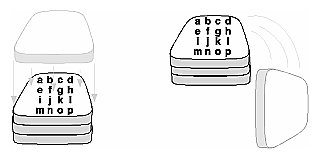
Similarly, for each wheel, you want to draw the wheel, remember where you are, and successively translate to each of the positions that bolts are drawn, throwing away the transformations after each bolt is drawn. Since the transformations are stored as matrices, a matrix stack provides an ideal mechanism for doing this sort of successive remembering, translating, and throwing away. All the matrix operations that have been described so far (glLoadMatrix(), glMultMatrix(), glLoadIdentity() and the commands that create specific transformation matrices) deal with the current matrix, or the top matrix on the stack. You can control which matrix is on top with the commands that perform stack operations: glPushMatrix(), which copies the current matrix and adds the copy to the top of the stack, and glPopMatrix(), which discards the top matrix on the stack, as shown in Figure 3-21. (Remember that the current matrix is always the matrix on the top.) In effect, glPushMatrix() means "remember where you are" and glPopMatrix() means "go back to where you were."
Figure 3-21 : Pushing and Popping the Matrix Stack void glPushMatrix(void); Pushes all matrices in the current stack down one level. The current stack is determined by glMatrixMode(). The topmost matrix is copied, so its contents are duplicated in both the top and second-from-the-top matrix. If too many matrices are pushed, an error is generated. void glPopMatrix(void); Pops the top matrix off the stack, destroying the contents of the popped matrix. What was the second-from-the-top matrix becomes the top matrix. The current stack is determined by glMatrixMode(). If the stack contains a single matrix, calling glPopMatrix() generates an error. Example 3-4 draws an automobile, assuming the existence of routines that draw the car body, a wheel, and a bolt. Example 3-4 : Pushing and Popping the Matrix draw_wheel_and_bolts() {
long i; draw_wheel(); for(i=0;i<5;i++){
glPushMatrix(); glRotatef(72.0*i,0.0,0.0,1.0); glTranslatef(3.0,0.0,0.0); draw_bolt(); glPopMatrix(); } } draw_body_and_wheel_and_bolts() {
draw_car_body(); glPushMatrix(); glTranslatef(40,0,30); /*move to first wheel position*/ draw_wheel_and_bolts(); glPopMatrix(); glPushMatrix(); glTranslatef(40,0,-30); /*move to 2nd wheel position*/ draw_wheel_and_bolts(); glPopMatrix(); … /*draw last two wheels similarly*/ } This code assumes the wheel and bolt axes are coincident with the z-axis, that the bolts are evenly spaced every 72 degrees, 3 units (maybe inches) from the center of the wheel, and that the front wheels are 40 units in front of and 30 units to the right and left of the car's origin. A stack is more efficient than an individual matrix, especially if the stack is implemented in hardware. When you push a matrix, you don't need to copy the current data back to the main process, and the hardware may be able to copy more than one element of the matrix at a time. Sometimes you might want to keep an identity matrix at the bottom of the stack so that you don't need to call glLoadIdentity() repeatedly. The Modelview Matrix StackAs you've seen earlier in "Viewing and Modeling Transformations," the modelview matrix contains the cumulative product of multiplying viewing and modeling transformation matrices. Each viewing or modeling transformation creates a new matrix that multiplies the current modelview matrix; the result, which becomes the new current matrix, represents the composite transformation. The modelview matrix stack contains at least thirty-two 4 × 4 matrices; initially, the topmost matrix is the identity matrix. Some implementations of OpenGL may support more than thirty-two matrices on the stack. To find the maximum allowable number of matrices, you can use the query command glGetIntegerv(GL_MAX_MODELVIEW_STACK_DEPTH, GLint *params). The Projection Matrix StackThe projection matrix contains a matrix for the projection transformation, which describes the viewing volume. Generally, you don't want to compose projection matrices, so you issue glLoadIdentity() before performing a projection transformation. Also for this reason, the projection matrix stack need be only two levels deep; some OpenGL implementations may allow more than two 4 × 4 matrices. To find the stack depth, call glGetIntegerv(GL_MAX_PROJECTION_STACK_DEPTH, GLint *params). One use for a second matrix in the stack would be an application that needs to display a help window with text in it, in addition to its normal window showing a three-dimensional scene. Since text is most easily positioned with an orthographic projection, you could change temporarily to an orthographic projection, display the help, and then return to your previous projection: glMatrixMode(GL_PROJECTION); glPushMatrix(); /*save the current projection*/ glLoadIdentity(); glOrtho(…); /*set up for displaying help*/ display_the_help(); glPopMatrix(); Note that you'd probably have to also change the modelview matrix appropriately. Advanced If you know enough mathematics, you can create custom projection matrices that perform arbitrary projective transformations. For example, the OpenGL and its Utility Library have no built-in mechanism for two-point perspective. If you were trying to emulate the drawings in drafting texts, you might need such a projection matrix. |