Viewport Transformation

Recalling the camera analogy, you know that the viewport transformation corresponds to the stage where the size of the developed photograph is chosen. Do you want a wallet-size or a poster-size photograph? Since this is computer graphics, the viewport is the rectangular region of the window where the image is drawn. Figure 3-16 shows a viewport that occupies most of the screen. The viewport is measured in window coordinates, which reflect the position of pixels on the screen relative to the lower-left corner of the window. Keep in mind that all vertices have been transformed by the modelview and projection matrices by this point, and vertices outside the viewing volume have been clipped.

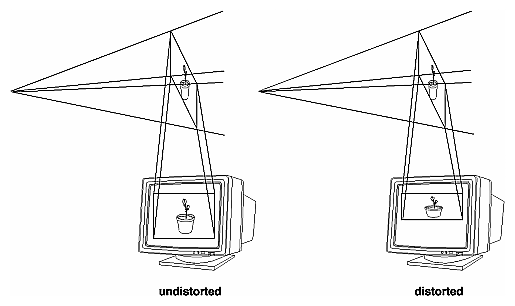
Figure 3-16 : Viewport Rectangle

Defining the Viewport

The window system, not OpenGL, is responsible for opening a window on the screen. However, by default the viewport is set to the entire pixel rectangle of the window that's opened. You use the glViewport() command to choose a smaller drawing region; for example, you can subdivide the window to create a split-screen effect for multiple views in the same window.

void glViewport(GLint x, GLint y, GLsizei width, GLsizei height);

Defines a pixel rectangle in the window into which the final image is mapped. The (x, y) parameter specifies the lower-left corner of the viewport, and width and height are the size of the viewport rectangle. By default, the initial viewport values are (0, 0, winWidth, winHeight), where winWidth and winHeight are the size of the window.

The aspect ratio of a viewport should generally equal the aspect ratio of the viewing volume. If the two ratios are different, the projected image will be distorted when mapped to the viewport, as shown in Figure 3-17. Note that subsequent changes to the size of the window don't explicitly affect the viewport. Your application should detect window resize events and modify the viewport appropriately.

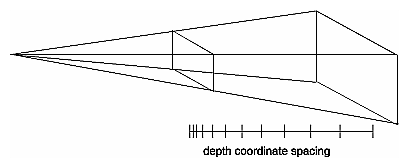
Figure 3-17 : Mapping the Viewing Volume to the Viewport

In Figure 3-17, the left figure shows a projection that maps a square image onto a square viewport using these routines:

gluPerspective(fovy, 1.0, near, far);

glViewport(0, 0, 400, 400);

However, in the right figure, the window has been resized to a nonequilateral rectangular viewport, but the projection is unchanged. The image appears compressed along the x-axis.

gluPerspective(fovy, 1.0, near, far);

glViewport (0, 0, 400, 200);

To avoid the distortion, modify the aspect ratio of the projection to match the viewport:

gluPerspective(fovy, 2.0, near, far);

glViewport(0, 0, 400, 200);

Try This

Modify an existing program so that an object is drawn twice, in different viewports. You might draw the object with different projection and/or viewing transformations for each viewport. To create two side-by-side viewports, you might issue these commands, along with the appropriate modeling, viewing, and projection transformations:

glViewport (0, 0, sizex/2, sizey);

                    .

                    .

                    .

glViewport (sizex/2, 0, sizex/2, sizey);

The Transformed Depth Coordinate

The depth (z) coordinate is encoded during the viewport transformation (and later stored in the depth buffer). You can scale z values to lie within a desired range with the glDepthRange() command. (Chapter 10 discusses the depth buffer and the corresponding uses for the depth coordinate.) Unlike x and y window coordinates, z window coordinates are treated by OpenGL as though they always range from 0.0 to 1.0.

void glDepthRange(GLclampd near, GLclampd far);

Defines an encoding for z coordinates that's performed during the viewport transformation. The near and far values represent adjustments to the minimum and maximum values that can be stored in the depth buffer. By default, they're 0.0 and 1.0, respectively, which work for most applications. These parameters are clamped to lie within [0,1].

In perspective projection, the transformed depth coordinate (like the x and y coordinates) is subject to perspective division by the w coordinate. As the transformed depth coordinate moves farther away from the near clipping plane, its location becomes increasingly less precise. (See Figure 3-18.)

Figure 3-18 : Perspective Projection and Transformed Depth Coordinates

Therefore, perspective division affects the accuracy of operations which rely upon the transformed depth coordinate, especially depth-buffering, which is used for hidden surface removal.