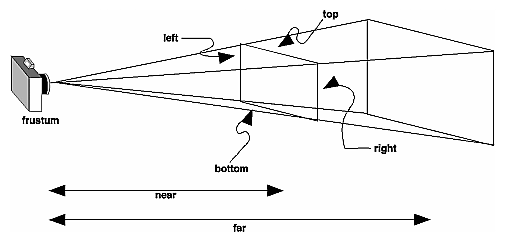
Projection Transformations

The previous section described how to compose the desired modelview matrix so that the correct modeling and viewing transformations are applied. This section explains how to define the desired projection matrix, which is also used to transform the vertices in your scene. Before you issue any of the transformation commands described in this section, remember to call

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

so that the commands affect the projection matrix rather than the modelview matrix and so that you avoid compound projection transformations. Since each projection transformation command completely describes a particular transformation, typically you don't want to combine a projection transformation with another transformation.

The purpose of the projection transformation is to define a viewing volume, which is used in two ways. The viewing volume determines how an object is projected onto the screen (that is, by using a perspective or an orthographic projection), and it defines which objects or portions of objects are clipped out of the final image. You can think of the viewpoint we've been talking about as existing at one end of the viewing volume. At this point, you might want to reread "A Simple Example: Drawing a Cube" for its overview of all the transformations, including projection transformations.

Perspective Projection

The most unmistakable characteristic of perspective projection is foreshortening: the farther an object is from the camera, the smaller it appears in the final image. This occurs because the viewing volume for a perspective projection is a frustum of a pyramid (a truncated pyramid whose top has been cut off by a plane parallel to its base). Objects that fall within the viewing volume are projected toward the apex of the pyramid, where the camera or viewpoint is. Objects that are closer to the viewpoint appear larger because they occupy a proportionally larger amount of the viewing volume than those that are farther away, in the larger part of the frustum. This method of projection is commonly used for animation, visual simulation, and any other applications that strive for some degree of realism because it's similar to how our eye (or a camera) works.

The command to define a frustum, glFrustum(), calculates a matrix that accomplishes perspective projection and multiplies the current projection matrix (typically the identity matrix) by it. Recall that the viewing volume is used to clip objects that lie outside of it; the four sides of the frustum, its top, and its base correspond to the six clipping planes of the viewing volume, as shown in Figure 3-13. Objects or parts of objects outside these planes are clipped from the final image. Note that glFrustum() doesn't require you to define a symmetric viewing volume.

Figure 3-13 : Perspective Viewing Volume Specified by glFrustum()

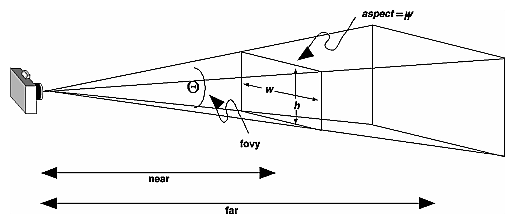
void glFrustum(GLdouble left, GLdouble right, GLdouble bottom,
GLdouble top, GLdouble near, GLdouble far);

Creates a matrix for a perspective-view frustum and multiplies the current matrix by it. The frustum's viewing volume is defined by the parameters: (left, bottom, -near) and (right, top, -near) specify the (x, y, z) coordinates of the lower-left and upper-right corners of the near clipping plane; near and far give the distances from the viewpoint to the near and far clipping planes. They should always be positive.

The frustum has a default orientation in three-dimensional space. You can perform rotations or translations on the projection matrix to alter this orientation, but this is tricky and nearly always avoidable.

Advanced

Also, the frustum doesn't have to be symmetrical, and its axis isn't necessarily aligned with the z-axis. For example, you can use glFrustum() to draw a picture as if you were looking through a rectangular window of a house, where the window was above and to the right of you. Photographers use such a viewing volume to create false perspectives. You might use it to have the hardware calculate images at much higher than normal resolutions, perhaps for use on a printer. For example, if you want an image that has twice the resolution of your screen, draw the same picture four times, each time using the frustum to cover the entire screen with one-quarter of the image. After each quarter of the image is rendered, you can read the pixels back to collect the data for the higher-resolution image. (See Chapter 8 for more information about reading pixel data.)

Although it's easy to understand conceptually, glFrustum() isn't intuitive to use. Instead, you might try the Utility Library routine gluPerspective(). This routine creates a viewing volume of the same shape as glFrustum() does, but you specify it in a different way. Rather than specifying corners of the near clipping plane, you specify the angle of the field of view ( &THgr; , or theta, in Figure 3-14) in the y direction and the aspect ratio of the width to height (x/y). (For a square portion of the screen, the aspect ratio is 1.0.) These two parameters are enough to determine an untruncated pyramid along the line of sight, as shown in Figure 3-14. You also specify the distance between the viewpoint and the near and far clipping planes, thereby truncating the pyramid. Note that gluPerspective() is limited to creating frustums that are symmetric in both the x- and y-axes along the line of sight, but this is usually what you want.

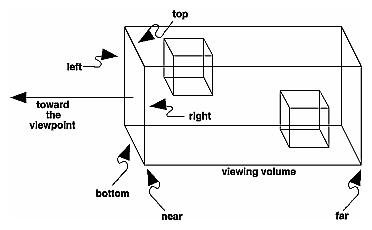
Figure 3-14 : Perspective Viewing Volume Specified by gluPerspective()

void gluPerspective(GLdouble fovy, GLdouble aspect,
GLdouble near, GLdouble far);

Creates a matrix for a symmetric perspective-view frustum and multiplies the current matrix by it. fovy is the angle of the field of view in the x-z plane; its value must be in the range [0.0,180.0]. aspect is the aspect ratio of the frustum, its width divided by its height. near and far values the distances between the viewpoint and the clipping planes, along the negative z-axis. They should always be positive.

Just as with glFrustum(), you can apply rotations or translations to change the default orientation of the viewing volume created by gluPerspective(). With no such transformations, the viewpoint remains at the origin, and the line of sight points down the negative z-axis.

With gluPerspective(), you need to pick appropriate values for the field of view, or the image may look distorted. For example, suppose you're drawing to the entire screen, which happens to be 11 inches high. If you choose a field of view of 90 degrees, your eye has to be about 7.8 inches from the screen for the image to appear undistorted. (This is the distance that makes the screen subtend 90 degrees.) If your eye is farther from the screen, as it usually is, the perspective doesn't look right. If your drawing area occupies less than the full screen, your eye has to be even closer. To get a perfect field of view, figure out how far your eye normally is from the screen and how big the window is, and calculate the angle the window subtends at that size and distance. It's probably smaller than you would guess. Another way to think about it is that a 94-degree field of view with a 35-millimeter camera requires a 20-millimeter lens, which is a very wide-angle lens. (See "Troubleshooting Transformations" for more details on how to calculate the desired field of view.)

The preceding paragraph mentions inches and millimeters - do these really have anything to do with OpenGL? The answer is, in a word, no. The projection and other transformations are inherently unitless. If you want to think of the near and far clipping planes as located at 1.0 and 20.0 meters, inches, kilometers, or leagues, it's up to you. The only rule is that you have to use a consistent unit of measurement. Then the resulting image is drawn to scale.

Orthographic Projection

With an orthographic projection, the viewing volume is a rectangular parallelepiped, or more informally, a box (see Figure 3-15). Unlike perspective projection, the size of the viewing volume doesn't change from one end to the other, so distance from the camera doesn't affect how large an object appears. This type of projection is used for applications such as creating architectural blueprints and computer-aided design, where it's crucial to maintain the actual sizes of objects and angles between them as they're projected.

Figure 3-15 : Orthographic Viewing Volume

The command glOrtho() creates an orthographic parallel viewing volume. As with glFrustum(), you specify the corners of the near clipping plane and the distance to the far clipping plane.

void glOrtho(GLdouble left, GLdouble right, GLdouble bottom,
GLdouble top, GLdouble near, GLdouble far);

Creates a matrix for an orthographic parallel viewing volume and multiplies the current matrix by it. (left, bottom, -near) and (right, top, -near) are points on the near clipping plane that are mapped to the lower-left and upper-right corners of the viewport window, respectively. (left, bottom, -far) and (right, top, -far) are points on the far clipping plane that are mapped to the same respective corners of the viewport. Both near and far can be positive or negative.

With no other transformations, the direction of projection is parallel to the z-axis, and the viewpoint faces toward the negative z-axis. Note that this means that the values passed in for far and near are used as negative z values if these planes are in front of the viewpoint, and positive if they're behind the viewpoint.

For the special case of projecting a two-dimensional image onto a two-dimensional screen, use the Utility Library routine gluOrtho2D(). This routine is identical to the three-dimensional version, glOrtho(), except that all the z coordinates for objects in the scene are assumed to lie between -1.0 and 1.0. If you're drawing two-dimensional objects using the two-dimensional vertex commands, all the z coordinates are zero; thus, none of the objects are clipped because of their z values.

void gluOrtho2D(GLdouble left, GLdouble right,
GLdouble bottom, GLdouble top);

Creates a matrix for projecting two-dimensional coordinates onto the screen and multiplies the current projection matrix by it. The clipping region is a rectangle with the lower-left corner at (left, bottom) and the upper-right corner at (right, top).

Viewing Volume Clipping

After the vertices of the objects in the scene have been transformed by the modelview and projection matrices, any primitives that lie outside the viewing volume are clipped. The six clipping planes used are those that define the sides and ends of the viewing volume. You can specify additional clipping planes and locate them wherever you choose. (See "Additional Clipping Planes" for information about this relatively advanced topic.) Keep in mind that OpenGL reconstructs the edges of polygons that get clipped.